题目内容
18.若实数x,y满足|x-3|≤y≤1,则z=$\frac{2x+y}{x+y}$的最小值为$\frac{5}{3}$.分析 把已知的不等式转化为不等式组,然后作出可行域,化目标函数为含有$\frac{y}{x}$的代数式,然后由$\frac{y}{x}$的几何意义求出其范围,代入目标函数求得目标函数的最小值.
解答 解:依题意,得实数x,y满足$\left\{\begin{array}{l}{x+y-3≥0}\\{x-y-3≤0}\\{0≤y≤1}\end{array}\right.$,画出可行域如图所示,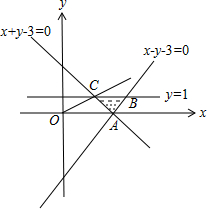
其中A(3,0),C(2,1),
z=$\frac{2x+y}{x+y}$=$\frac{x+y}{x+y}+\frac{x}{x+y}=1+\frac{1}{1+\frac{y}{x}}$,
设k=$\frac{y}{x}$,则k的几何意义为区域内的点与原点的斜率,
则OC的斜率最大为k=$\frac{1}{2}$,OA的斜率最小为k=0,
则0≤k≤$\frac{1}{2}$,则1≤k+1≤$\frac{3}{2}$,$\frac{2}{3}$≤$\frac{1}{1+\frac{y}{x}}$≤1,
故$\frac{5}{3}$≤1+$\frac{1}{1+\frac{y}{x}}$≤2,
故z=$\frac{2x+y}{x+y}$的最小值为$\frac{5}{3}$.
故答案为:$\frac{5}{3}$.
点评 本题主要考查线性规划的应用以及直线斜率的应用,利用数形结合是解决本题的关键.是中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
15.下列函数中,既是奇函数又在其定义域上是增函数的是( )
| A. | $y=-\frac{2}{x}$ | B. | y=x3 | C. | y=log2x | D. | y=tanx |
7.设x,y满足约束条件$\left\{\begin{array}{l}{x+y≤1}\\{x+1≥0}\\{x-y≤1}\end{array}\right.$,则目标函数z=$\frac{y}{x-2}$的取值范围为( )
| A. | [-3,3] | B. | [-2,2] | C. | [-1,1] | D. | [-$\frac{2}{3}$,$\frac{2}{3}$] |
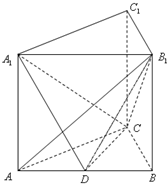 如图、已知直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.
如图、已知直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.