题目内容
【题目】已知抛物线C：
，过焦点F的直线l与抛物线C交于M，N两点.
（1）若直线l的倾斜角为
，求
的长；
（2）设M在准线上的射影为A，求证：A，O，N三点共线（O为坐标原点）.
【答案】（1）8；（2）见解析
【解析】
（1）由题意知直线l的方程，与抛物线联立求出两根之和及两根之积，进而求出弦长
：
（2）设直线l的方程与抛物线联立求出两根之积，得出纵坐标之间的关系，求出
，
的斜率，值相等，结合两直线有公共点O可得三点共线.
解：（1）由题意知抛物线的焦点
，直线l的倾斜角为
，则直线的斜率为1，
所以直线l的方程：
，设
，
，联立直线与抛物线的方程整理得：
，
所以
，
，
所以弦长
，
所以
的长为8；
（2）显然直线l的斜率不为0，设直线方程为：
，设，，由题意知
，
联立直线与抛物线的方程整理为：
，
，，
因为
，
∴
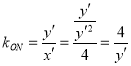
，，又有公共点
，
所以A，O，N三点共线.
练习册系列答案
相关题目
