��Ŀ����
��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣����ڴ���ָֽ�����������𣬽��Ӧд������˵����֤�����̻����㲽�裮A��ѡ��4-1��������֤��ѡ����
��ͼ����O��һ��P��ԲO���������ߣ��е�ֱ�ΪA��B��
AB��OP���ڵ�M����CDΪ����M�Ҳ���Բ��O��һ���ң�
��֤��O��C��P��D�ĵ㹲Բ��
B��ѡ��4-2����������任��
��֪������M������ֵ��=3����Ӧ��һ����������e1=[
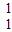 ]�����Ҿ���M��Ӧ�ı任���㣨-1��2���任�ɣ�9��15���������M��
]�����Ҿ���M��Ӧ�ı任���㣨-1��2���任�ɣ�9��15���������M��C��ѡ��4-4��������ϵ��������̣�
�ڼ�����ϵ�У�����C�ļ����귽��Ϊp=2
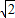 sin��
sin��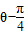 �����Լ���Ϊԭ�㣬����Ϊx��������Ὠ��ƽ��ֱ������ϵ��ֱ��l�IJ�������Ϊ
�����Լ���Ϊԭ�㣬����Ϊx��������Ὠ��ƽ��ֱ������ϵ��ֱ��l�IJ�������Ϊ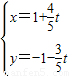 ��tΪ����������ֱ��l������C���صõ��ҳ���
��tΪ����������ֱ��l������C���صõ��ҳ���D��ѡ��4-5������ʽѡ����
��֪ʵ��x��y��z����x+y+z=2����2x2+3y2+z2����Сֵ��

���𰸡�������A����ΪPA��PBΪԲO���������ߣ�����OP��ֱƽ����AB����Rt��OAP�У�OM•MP=AM2��ԲO�У�AM•BM=CM•DM���ɴ��ܹ�֤��O��C��P��D�ĵ㹲Բ��
B����M= ����
����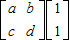 =3
=3 =
= ��
�� =
= ���ɴ������M��
���ɴ������M��
C������=2 sin��
sin�� ����
����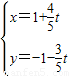 �ֱ�Ϊ��ͨ���̣�x2+y2+2x-2y=0��3x+4y+1=0���ɴ�������ҳ���
�ֱ�Ϊ��ͨ���̣�x2+y2+2x-2y=0��3x+4y+1=0���ɴ�������ҳ���
D���ɿ�������ʽ֪����x+y+z��2��[��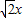 ��2+��
��2+��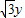 ��2+z2]•[��
��2+z2]•[��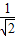 ��2+��
��2+��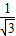 ��2+12]����
��2+12]���� ���ɴ������2x2+3y2+z2����Сֵ��
���ɴ������2x2+3y2+z2����Сֵ��
��� A��ѡ��4-1��������֤��ѡ����
A��ѡ��4-1��������֤��ѡ����
֤������ΪPA��PBΪԲO���������ߣ�
����OP��ֱƽ����AB��
��Rt��OAP�У�OM•MP=AM2������4�֣�
��ԲO�У�AM•BM=CM•DM��
����OM•MP=CM•DM������8�֣�
����CD����Բ��O������O��C��P��D�ĵ㹲Բ������10�֣�
B��ѡ��4-2����������任��
��M= ����
���� =3
=3 =
= ��
��
�� ������4�֣�
������4�֣�
 =
= ����
���� ������7�֣�
������7�֣�
������������������a=-1��b=4��c=-3��d=6��
��M= �� ����10�֣�
�� ����10�֣�
C��ѡ��4-4��������ϵ��������̣�
�⣺�����̦�=2 sin��
sin��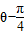 ����
���� �ֱ�Ϊ��ͨ���̣�
�ֱ�Ϊ��ͨ���̣�
x2+y2+2x-2y=0��3x+4y+1=0������6�֣�
������C��Բ��ΪC��-1��1�����뾶Ϊ ��
��
����Բ��C��ֱ��l�ľ���Ϊ ��
��
�������ҳ�Ϊ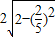 =
= ������10�֣�
������10�֣�
D��ѡ��4-5������ʽѡ����
�⣺�ɿ�������ʽ��֪��
��x+y+z��2��[�� ��2+��
��2+�� ��2+z2]•[��
��2+z2]•[�� ��2+��
��2+�� ��2+12]������5�֣�
��2+12]������5�֣�
�� ��
��
���ҽ���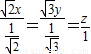 ��
��
����x= ��y=
��y= ��z=
��z=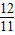 ʱ��
ʱ��
2x2+3y2+z2ȡ����СֵΪ ������10�֣�
������10�֣�
������A������Բ�йصı����߶ε�Ӧ�ã�B���������任��Ӧ�ã�C���鼫������������̵�Ӧ�ã�D�����������ʽ��Ӧ�ã�����ʱҪ�������⣬��ϸ���ע��ȼ�ת��˼���������ã�
B����M=
 ����
����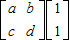 =3
=3 =
= ��
�� =
= ���ɴ������M��
���ɴ������M��C������=2
 sin��
sin�� ����
����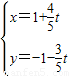 �ֱ�Ϊ��ͨ���̣�x2+y2+2x-2y=0��3x+4y+1=0���ɴ�������ҳ���
�ֱ�Ϊ��ͨ���̣�x2+y2+2x-2y=0��3x+4y+1=0���ɴ�������ҳ���D���ɿ�������ʽ֪����x+y+z��2��[��
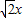 ��2+��
��2+��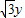 ��2+z2]•[��
��2+z2]•[��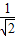 ��2+��
��2+��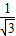 ��2+12]����
��2+12]���� ���ɴ������2x2+3y2+z2����Сֵ��
���ɴ������2x2+3y2+z2����Сֵ�����
 A��ѡ��4-1��������֤��ѡ����
A��ѡ��4-1��������֤��ѡ����֤������ΪPA��PBΪԲO���������ߣ�
����OP��ֱƽ����AB��
��Rt��OAP�У�OM•MP=AM2������4�֣�
��ԲO�У�AM•BM=CM•DM��
����OM•MP=CM•DM������8�֣�
����CD����Բ��O������O��C��P��D�ĵ㹲Բ������10�֣�
B��ѡ��4-2����������任��
��M=
 ����
���� =3
=3 =
= ��
����
 ������4�֣�
������4�֣� =
= ����
���� ������7�֣�
������7�֣�������������������a=-1��b=4��c=-3��d=6��
��M=
 �� ����10�֣�
�� ����10�֣�C��ѡ��4-4��������ϵ��������̣�
�⣺�����̦�=2
 sin��
sin��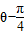 ����
���� �ֱ�Ϊ��ͨ���̣�
�ֱ�Ϊ��ͨ���̣�x2+y2+2x-2y=0��3x+4y+1=0������6�֣�
������C��Բ��ΪC��-1��1�����뾶Ϊ
 ��
������Բ��C��ֱ��l�ľ���Ϊ
 ��
���������ҳ�Ϊ
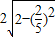 =
= ������10�֣�
������10�֣�D��ѡ��4-5������ʽѡ����
�⣺�ɿ�������ʽ��֪��
��x+y+z��2��[��
 ��2+��
��2+�� ��2+z2]•[��
��2+z2]•[�� ��2+��
��2+�� ��2+12]������5�֣�
��2+12]������5�֣���
 ��
�����ҽ���
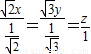 ��
������x=
 ��y=
��y= ��z=
��z=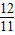 ʱ��
ʱ��2x2+3y2+z2ȡ����СֵΪ
 ������10�֣�
������10�֣�������A������Բ�йصı����߶ε�Ӧ�ã�B���������任��Ӧ�ã�C���鼫������������̵�Ӧ�ã�D�����������ʽ��Ӧ�ã�����ʱҪ�������⣬��ϸ���ע��ȼ�ת��˼���������ã�

��ϰ��ϵ�д�
�����Ŀ
 ��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣����ڴ���ָֽ�������� ���𣮽��Ӧд������˵����֤�����̻����㲽�裮
��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣����ڴ���ָֽ�������� ���𣮽��Ӧд������˵����֤�����̻����㲽�裮 ѡ������A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣�
ѡ������A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣� ��ѡ���⣩��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣����ڴ��ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裮
��ѡ���⣩��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣����ڴ��ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裮 ѡ���⣺��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣���20�֣����Ӧд������˵����֤�����̻����㲽�裮
ѡ���⣺��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣���20�֣����Ӧд������˵����֤�����̻����㲽�裮 ѡ���⣨��A��B��C��D��С����ֻ��ѡ�����⣬����ѡ�������2BǦ��Ϳ�ڣ�ÿС��10�֣���20�֣����ڴ���ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裩��
ѡ���⣨��A��B��C��D��С����ֻ��ѡ�����⣬����ѡ�������2BǦ��Ϳ�ڣ�ÿС��10�֣���20�֣����ڴ���ָ�����������𣬽��ʱӦд������˵����֤�����̻����㲽�裩��