题目内容
已知三棱锥V-ABC,底面是边长为2的正三角形,VA⊥底面△ABC,VA=2,D是VB中点,则异面直线VC、AD所成角的大小为 (用反三角函数表示).
【答案】分析:先根据题意作出图形,取BC的中点E,连接AE,DE,得出∠ADE是异面直线VC、AD所成角,在△ADE中,由余弦定理得cos∠ADE从而得出异面直线VC、AD所成角的大小为.
解答: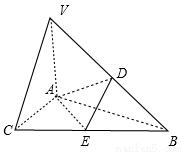 解:取BC的中点E,连接AE,DE,
解:取BC的中点E,连接AE,DE,
则DE∥VC,故∠ADE是异面直线VC、AD所成角,
在△ADE中,AD=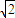 .DE=
.DE= VC=
VC=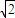 ,AE=
,AE=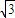 ,
,
由余弦定理得:cos∠ADE=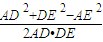 =
=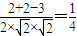
∴∠ADE=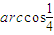 ,
,
则异面直线VC、AD所成角的大小为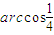 ,
,
故答案为: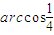 (等).
(等).
点评:本小题主要考查异面直线所成角、反三角函数的运用、解三角形等基础知识,考查运算求解能力,考查空间想象力.属于基础题.
解答:
 解:取BC的中点E,连接AE,DE,
解:取BC的中点E,连接AE,DE,则DE∥VC,故∠ADE是异面直线VC、AD所成角,
在△ADE中,AD=
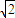 .DE=
.DE= VC=
VC=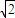 ,AE=
,AE=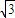 ,
,由余弦定理得:cos∠ADE=
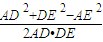 =
=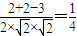
∴∠ADE=
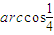 ,
,则异面直线VC、AD所成角的大小为
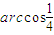 ,
,故答案为:
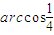 (等).
(等).点评:本小题主要考查异面直线所成角、反三角函数的运用、解三角形等基础知识,考查运算求解能力,考查空间想象力.属于基础题.

练习册系列答案
相关题目
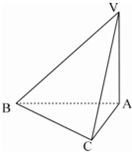 如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.
如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.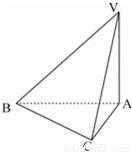 如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.
如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.