题目内容
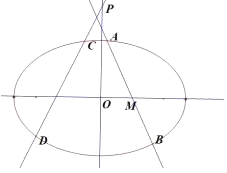
【题目】用一个半径为12厘米圆心角为![]() 的扇形纸片PAD卷成一个侧面积最大的无底圆锥(接口不用考虑损失),放于水平面上.
的扇形纸片PAD卷成一个侧面积最大的无底圆锥(接口不用考虑损失),放于水平面上.
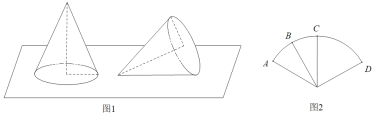
(1)无底圆锥被一阵风吹倒后(如图1),求它的最高点到水平面的距离;
(2)扇形纸片PAD上(如图2),C是弧AD的中点,B是弧AC的中点,卷成无底圆锥后,求异面直线PA与BC所成角的大小.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)如图,设![]() 为轴截面,过点
为轴截面,过点![]() 作
作![]() 于点
于点![]() ,在
,在![]() 中求出
中求出![]() 的长度即为所求;
的长度即为所求;
(2)先求出![]() ,利用夹角公式求出
,利用夹角公式求出![]() ,进而可得异面直线PA与BC所成角的大小.
,进而可得异面直线PA与BC所成角的大小.
(1)如图所示,

设![]() 为轴截面,过点
为轴截面,过点![]() 作
作![]() 于点
于点![]() ,
,
则![]() ,解得
,解得![]() ,
,
所以在![]() 中,
中,![]() ,
,
![]()
![]() ,
,
即无底圆锥被一阵风吹倒后(如图1),它的最高点到水平面的距离为![]() ,
,
(2)如图:

因为B是弧AC的中点,所以三角形![]() 为等腰直角三角形,
为等腰直角三角形,
则由(1)得![]() ,且
,且![]() 面
面![]() ,
,
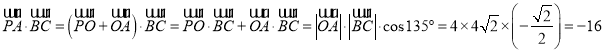
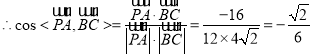 ,
,
![]() 异面直线PA与BC所成角的大小为
异面直线PA与BC所成角的大小为![]() .
.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目