题目内容
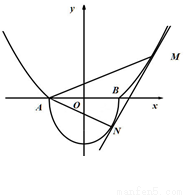
如图所示的曲线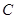 是由部分抛物线
是由部分抛物线 和曲线
和曲线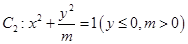 “合成”的,直线
“合成”的,直线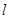 与曲线
与曲线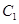 相切于点
相切于点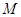 ,与曲线
,与曲线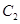 相切于点
相切于点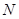 ,记点
,记点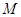 的横坐标为
的横坐标为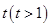 ,其中
,其中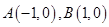 .
.
(1)当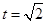 时,求
时,求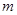 的值和点
的值和点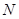 的坐标;
的坐标;
(2)当实数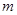 取何值时,
取何值时,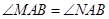 ?并求出此时直线
?并求出此时直线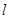 的方程.
的方程.
【答案】
(1) 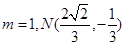 (2)
(2) 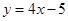
【解析】
试题分析:解:(1)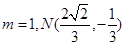
(2)由题意可知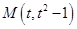 ,切线
,切线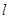 的斜率为
的斜率为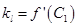
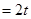 ,
, 切线
切线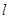 的方程表达式为
的方程表达式为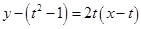 ,即
,即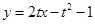 ,与
,与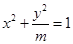 联立方程组,整理得
联立方程组,整理得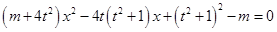 (①).此时
(①).此时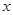 为点
为点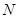 的横坐标.
的横坐标.
 直线
直线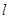 与曲线
与曲线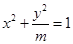
 相切于点
相切于点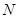 ,
,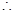
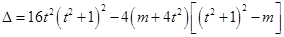
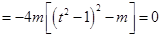 ,解得
,解得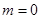 (舍)或
(舍)或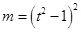 ,点
,点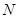 的坐标为
的坐标为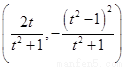 .
.
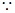
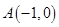 ,
,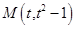 ,
, 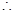
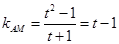 ,
,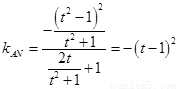 ,
,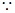
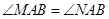 ,则
,则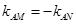 ,
,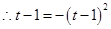 .
.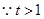 ,
,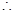
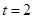 .由(1)可知
.由(1)可知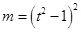 ,
,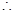
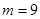 .把
.把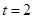 代入点
代入点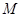 和点
和点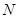 ,解得
,解得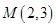 ,
, ,
,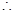
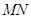 所在直线的方程为
所在直线的方程为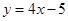 .
.
考点:直线与抛物线的位置关系
点评:解决的关键是利用直线与曲线相切,联立方程组得到判别式等于零,进而得到m的值,公式得到点N的坐标,,对于角的相等的求解,一般结合斜率来完成,属于中档题。

练习册系列答案
相关题目
 5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )
5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )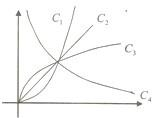 如图所示的曲线是幂函数y=xn在第一象限内的图象.已知n分别取-1,l,
如图所示的曲线是幂函数y=xn在第一象限内的图象.已知n分别取-1,l,| 1 |
| 2 |
A、2,1,
| ||
B、2,-1,1,
| ||
C、
| ||
D、-1,1,2,
|
 6、如图所示的图形是由若干个小正方体所叠成的几何体的侧(左)视图与俯视图,其中俯视图的小正方形中的数字表示该几何体在同一位置上叠放的小正方形的个数,则这个几何体的正(主)试图是( )
6、如图所示的图形是由若干个小正方体所叠成的几何体的侧(左)视图与俯视图,其中俯视图的小正方形中的数字表示该几何体在同一位置上叠放的小正方形的个数,则这个几何体的正(主)试图是( ) 已知:如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的,其中AB=4,BC=2,CG=3,BE=1,
已知:如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的,其中AB=4,BC=2,CG=3,BE=1,