题目内容

5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成，现用3种不同颜色对这个几何体的表面染色（底面A1B1C1不涂色），要求相邻的面均不同色，则不同的染色方案共有（　　）
分析：根据题意，分两步进行；先涂三棱锥P-ABC的三个侧面，然后涂三棱柱的三个侧面，由分步计数原理，计算可得答案．
解答：解：先涂三棱锥P-ABC的三个侧面，有C13×C12种情况；
然后涂三棱柱的三个侧面，有C11×C12种情况；
共有C13×C12×C11×C12=3×2×1×2=12种不同的涂法．
故选D
点评：本题考查分步计数的原理的运用，注意分析题意，认清是分类问题还是分步问题．
练习册系列答案
相关题目
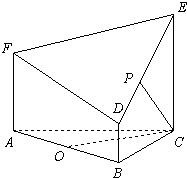精英家教网如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得，已知FA⊥平面ABC，AB=2，BD=1，AF=2，CE=3，O为AB的中点．
（Ⅰ）求平面DEF与平面ABC相交所成锐角二面角的余弦值；
（Ⅱ）在DE上是否存在一点P，使CP⊥平面DEF？如果存在，求出DP的长；若不存在，说明理由．
如图所示的几何体是由以正三角形ABC为底面的直棱柱被平面 DEF所截而得．AB=2，BD=1，CE=3，AF=a，O为AB的中点．
（1）当a=4时，求平面DEF与平面ABC的夹角的余弦值；
（2）当a为何值时，在棱DE上存在点P，使CP⊥平面DEF？
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得，已知FA⊥
平面ABC，AB=2，AF=2，CE=3，BD=1，O为BC的中点．
（1）求证：AO∥平面DEF；
（2）求证：平面DEF⊥平面BCED；
（3）求平面DEF与平面ABC相交所成锐角二面角的余弦值．
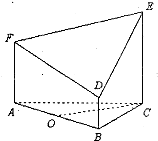如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得，已知FA⊥平面ABC，BD=1，AF=2，CE=3，O为AB的中点．
（1）求证：OC⊥DF；
（2）试问线段CE上是否存在一点P，使得OP∥平面DEF？若存在，求出CP的长度，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网