题目内容
 已知:如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的,其中AB=4,BC=2,CG=3,BE=1,
已知:如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的,其中AB=4,BC=2,CG=3,BE=1,(1)求:BF与平面BCGE所成角的正切值
(2)求:截面AEGF与平面ABCD所成的二面角的余弦值
(3)在线段CG上是否存在一点M,使得M在平面AEGF上的射影恰为△EGF的重心.
分析:(1)可以建立空间坐标系,设出F点的坐标,根据截面AEFG为平行四边形,
=
,得到F点的坐标;利用
与平面BCGE的法向量夹角求解.
(2)分别求出平面AEGF及平面FABCD的法向量,代入向量夹角公式,即可得到二面角E-FC1-C的余弦值.
(3)设M在平面AEGF的射影为H,
=
∴GM=
>3.故不存在.
| AF |
| EG |
| BF |
(2)分别求出平面AEGF及平面FABCD的法向量,代入向量夹角公式,即可得到二面角E-FC1-C的余弦值.
(3)设M在平面AEGF的射影为H,
| GM |
| AG |
| GH |
| GC |
| 29 |
| 9 |
解答: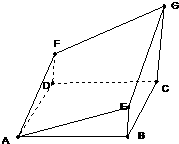 解:(1)建立如图所示的空间直角坐标系,
解:(1)建立如图所示的空间直角坐标系,
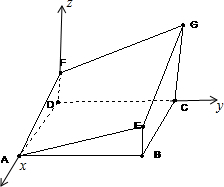
则D(0,0,0),B(2,4,0)A(2,0,0),C(0,4,0),E(2,4,1),G(0,4,3)设F(0,0,z).
∵AEGF为平行四边形,
∴
=
,
即(-2,0,z)=(-2,0,2),∴z=2.
∴F(0,0,2).
∴
=(-2,-4,2).于是|
|=2
,即BF的长为2
.
=(-2,-4,2),
易知平面BCGE的一个法向量为
=(0,1,0),|cos<
>|=
=
=sinθ
cosθ=
∴BF与平面BCGE所成角的正切值为tanθ=2.
(2)设
为平面AEGF的法向量且
=(x,y,z)
由
得
即
令z=1∴
,
=(1,-
,1),易知平面ABCD的法向量
=(0,0,1)
设截面AEGF与平面ABCD所成的二面角为α,则|cosα|=|
|=
(2)截面AEGF与平面ABCD所成的锐二面角的余弦值
.
(3)不存在,在△AGC中,设M在平面AEGF的射影为H,
∵
=
∴GM=
>3.故不存在.
 解:(1)建立如图所示的空间直角坐标系,
解:(1)建立如图所示的空间直角坐标系,
则D(0,0,0),B(2,4,0)A(2,0,0),C(0,4,0),E(2,4,1),G(0,4,3)设F(0,0,z).
∵AEGF为平行四边形,
∴
| AF |
| EG |
即(-2,0,z)=(-2,0,2),∴z=2.
∴F(0,0,2).
∴
| EF |
| BF |
| 6 |
| 6 |
| BF |
易知平面BCGE的一个法向量为
| m |
| BF, |
| m |
| 4 | ||
2
|
2
| ||
| 5 |
cosθ=
| ||
| 5 |
(2)设
| n1 |
| n1 |
由
|
|
即
|
|
| n1 |
| 1 |
| 4 |
| n2 |
设截面AEGF与平面ABCD所成的二面角为α,则|cosα|=|
| ||||
|
|
| 4 | ||
|
(2)截面AEGF与平面ABCD所成的锐二面角的余弦值
| 4 | ||
|
(3)不存在,在△AGC中,设M在平面AEGF的射影为H,
∵
| GM |
| AG |
| GH |
| GC |
| 29 |
| 9 |
点评:本题主要考查线线角,二面角空间角的计算.利用空间向量知识方法求解,思路稳定,使问题论证与计算变成了代数运算,使人们解决问题更加方便.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
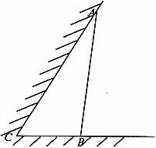
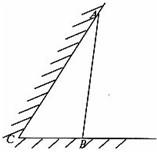 如图所示,某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室,已知已有的两面墙的夹角为60°(即∠C=60°且两面墙的长度足够大),现有可供建造第三面围墙的材料6米(即AB长为6米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记∠ABC=θ.
如图所示,某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室,已知已有的两面墙的夹角为60°(即∠C=60°且两面墙的长度足够大),现有可供建造第三面围墙的材料6米(即AB长为6米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记∠ABC=θ.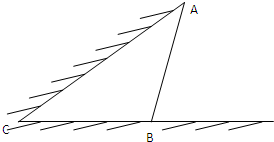 如图所示,某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室.已知已有两面墙的夹角为60°(即∠C=60°),第三面围墙的长度为6米,即AB=6米,(两面墙的长均大于6米).为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大.记∠ABC=θ,问当θ为多少时,所建造的三角形露天活动室的面积最大?
如图所示,某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室.已知已有两面墙的夹角为60°(即∠C=60°),第三面围墙的长度为6米,即AB=6米,(两面墙的长均大于6米).为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大.记∠ABC=θ,问当θ为多少时,所建造的三角形露天活动室的面积最大?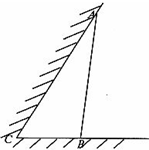 如图所示,某饲养场要建造一间两面靠墙的三角形露天养殖场,已知已有两面墙的夹角为60°(即∠C=60°),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记∠ABC=θ.
如图所示,某饲养场要建造一间两面靠墙的三角形露天养殖场,已知已有两面墙的夹角为60°(即∠C=60°),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记∠ABC=θ.