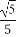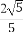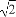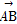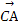题目内容
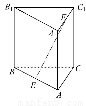
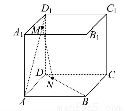
如图,三棱柱ABC-A1B1C1的所有棱长都是2,又AA1⊥平面ABC,D,E分别是AC,CC1的中点.

(1)求证:AE⊥平面A1BD.
(2)求二面角D-BA1-A的余弦值.
(3)求点B1到平面A1BD的距离.
(1)见解析 (2) 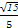 (3)
(3) 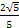
【解析】由AA1⊥平面ABC可知,平面ABC⊥平面ACC1A1,故可考虑建立空间直角坐标系解决问题.
【解析】
(1)以D为原点,DA所在直线为x轴,过D作AC的垂线为y轴,DB所在直线为z轴建立空间直角坐标系如图,
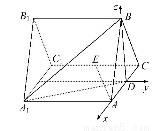
则A(1,0,0),C(-1,0,0),E(-1,-1,0),A1(1,-2,0),C1(-1,-2,0),B(0,0,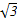 ),B1(0,-2,
),B1(0,-2,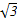 ),
),
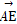 =(-2,-1,0),
=(-2,-1,0),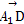 =(-1,2,0),
=(-1,2,0),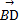 =(0,0,-
=(0,0,-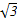 ).∴
).∴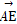 ·
·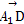 =2-2+0=0,
=2-2+0=0,
∴AE⊥A1D,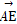 ·
·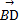 =0,∴AE⊥BD.
=0,∴AE⊥BD.
又A1D与BD相交于D,∴AE⊥平面A1BD.
(2)设平面DA1B的一个法向量为n1=(x1,y1,z1),
由 ⇒
⇒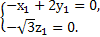 取n1=(2,1,0).
取n1=(2,1,0).
设平面AA1B的一个法向量为n2=(x2,y2,z2),
易得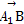 =(-1,2,
=(-1,2,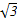 ),
),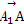 =(0,2,0),
=(0,2,0),
则由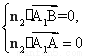 ⇒
⇒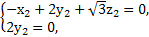
取n2=(3,0,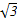 ).cos<n1,n2>=
).cos<n1,n2>=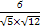 =
=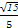 .
.
故二面角D-BA1-A的余弦值为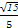 .
.
(3)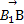 =(0,2,0),平面A1BD的法向量取n1=(2,1,0),则点B1到平面A1BD的距离为d=|
=(0,2,0),平面A1BD的法向量取n1=(2,1,0),则点B1到平面A1BD的距离为d=|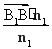 |=
|=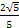 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目