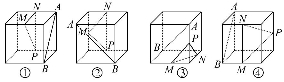
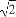题目内容
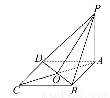
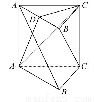
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点M在AD1上移动,点N在BD上移动,D1M=DN=a(0<a<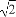 ),连接MN.
),连接MN.
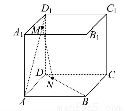
(1)证明对任意a∈(0,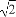 ),总有MN∥平面DCC1D1.
),总有MN∥平面DCC1D1.
(2)当a为何值时,MN的长最小?
(1)见解析 (2) 当a= 时,MN的长有最小值
时,MN的长有最小值
【解析】(1)作MP∥AD,交DD1于P,作NQ∥BC,交DC于Q,连接PQ.
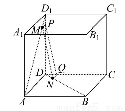
由题意得MP∥NQ,且MP=NQ,
则四边形MNQP为平行四边形.
∴MN∥PQ.
又PQ?平面DCC1D1,MN?平面DCC1D1,
∴MN∥平面DCC1D1.
(2)由(1)知四边形MNQP为平行四边形,
∴MN=PQ,
由已知D1M=DN=a,DD1=AD=DC=1,
∴AD1=BD=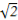 ,
,
∴D1P∶1=a∶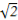 ,DQ∶1=a∶
,DQ∶1=a∶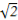 ,
,
即D1P=DQ=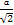 .
.
∴MN=PQ=
=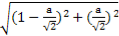
=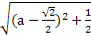 (0<a<
(0<a<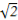 ),
),
故当a= 时,MN的长有最小值
时,MN的长有最小值 .
.
即当M,N分别移动到AD1,BD的中点时,MN的长最小,此时MN的长为 .
.

练习册系列答案
相关题目