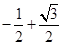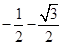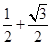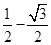题目内容
已知函数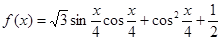
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)在锐角△ABC中,角A、B、C的对边分别是 、b、c满足
、b、c满足 ,求
,求 的取值范围.
的取值范围.
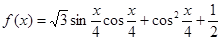
(Ⅰ)求
 的单调递增区间;
的单调递增区间; (Ⅱ)在锐角△ABC中,角A、B、C的对边分别是
 、b、c满足
、b、c满足 ,求
,求 的取值范围.
的取值范围.解:(Ⅰ)由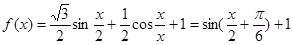 2分
2分
由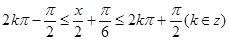
得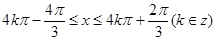
∴f(x)的单调递增区间为[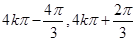 ](k∈Z) 5分
](k∈Z) 5分
(Ⅱ)由(2a-c)cosB=bcosC及正弦定理得(2sinA-sinC)cosB=sinBcosC
∴2sinAcosB=cosBsinC+sinBcosC=sin(B+C)
又∵A+B+C=π,∴sin(B+C)=sinA≠0
∴cosB=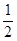 , 又
, 又 B=
B=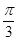 , 8分
, 8分
A+C=π-B=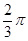 又∵A,C为锐角,∴
又∵A,C为锐角,∴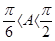 9分
9分
∴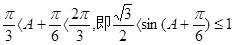 11分
11分
∴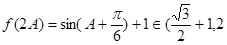 ]故
]故 的取值范围是(
的取值范围是(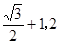 ]13分
]13分
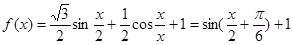 2分
2分由
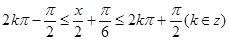
得
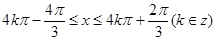
∴f(x)的单调递增区间为[
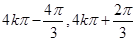 ](k∈Z) 5分
](k∈Z) 5分(Ⅱ)由(2a-c)cosB=bcosC及正弦定理得(2sinA-sinC)cosB=sinBcosC
∴2sinAcosB=cosBsinC+sinBcosC=sin(B+C)
又∵A+B+C=π,∴sin(B+C)=sinA≠0
∴cosB=
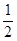 , 又
, 又 B=
B=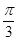 , 8分
, 8分A+C=π-B=
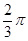 又∵A,C为锐角,∴
又∵A,C为锐角,∴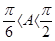 9分
9分∴
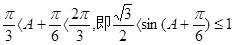 11分
11分∴
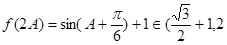 ]故
]故 的取值范围是(
的取值范围是(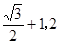 ]13分
]13分略

练习册系列答案
相关题目
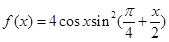
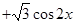
 .
.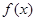 的最小正周期;(Ⅱ)若
的最小正周期;(Ⅱ)若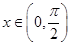 ,求
,求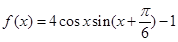 .
.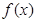 的最小正周期及
的最小正周期及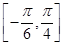 上的最大值和最小值.
上的最大值和最小值.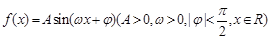 的图象的一部分如下图所示.
的图象的一部分如下图所示.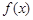 的解析式;
的解析式;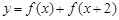 的最大值与最小值.
的最大值与最小值.
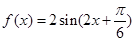 ,则函数
,则函数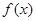 的单调递增区间是
的单调递增区间是 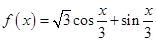 的最小正周期为 .
的最小正周期为 .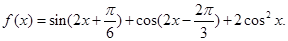
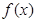 的最大值和最小正周期;
的最大值和最小正周期;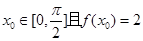 ,求
,求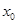 的值。
的值。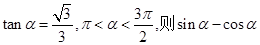 的值( )
的值( )