题目内容
已知椭圆C1的中心在坐标原点,两个焦点分别为F1(-2,0),F2(2,0),点A(2,3)在椭圆C1上,过点A的直线L与抛物线C2:x2=4y交于B,C两点,抛物线C2在点B,C处的切线分别为l1,l2,且l1与l2交于点P.
(1)求椭圆C1的方程;
(2)是否存在满足|PF1|+|PF2|=|AF1|+|AF2|的点P?若存在,指出这样的点P有几个(不必求出点P的坐标);若不存在,说明理由.
(1) +
+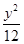 =1 (2)存在,有2个
=1 (2)存在,有2个
解析解:(1)设椭圆方程为 +
+ =1(a>b>0),
=1(a>b>0),
由题意可知2a=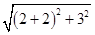 +
+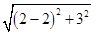 =8.
=8.
∴a=4,b2=a2-c2=12.
∴椭圆方程为 +
+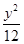 =1.
=1.
(2)设B(x1, ),C(x2,
),C(x2,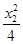 ),
),
直线BC的斜率为k,则k=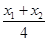 .
.
由y=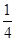 x2,得y′=
x2,得y′=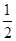 x.
x.
∴点B、C处的切线l1、l2的斜率分别为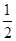 x1,
x1,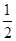 x2,
x2,
∴l1的方程为y- =
=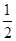 x1(x-x1),
x1(x-x1),
即y=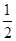 x1x-
x1x-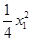 ,
,
同理,l2的方程为y=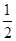 x2x-
x2x-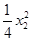 .
.
由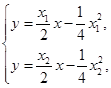
解得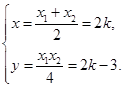
∴P(2k,2k-3).
∵|PF1|+|PF2|=|AF1|+|AF2|,
∴点P在椭圆C1: +
+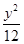 =1上,
=1上,
∴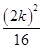 +
+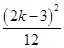 =1.
=1.
化简得7k2-12k-3=0.(*)
由Δ=122-4×7×(-3)=228>0,
可得方程(*)有两个不等的实数根.
∴满足条件的点P有两个.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 )的直线与椭圆交于A、B两点,与直线y=2交于点M(直线AB不经过P点),记PA、PB、PM的斜率分别为k1、k2、k3,问:是否存在常数
)的直线与椭圆交于A、B两点,与直线y=2交于点M(直线AB不经过P点),记PA、PB、PM的斜率分别为k1、k2、k3,问:是否存在常数 ,使得
,使得 若存在,求出名
若存在,求出名 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率 ,直线
,直线 交椭圆于M,N两点。
交椭圆于M,N两点。 ,求弦MN的长;
,求弦MN的长; :
: 的切线l,切点A在第二象限。
的切线l,切点A在第二象限。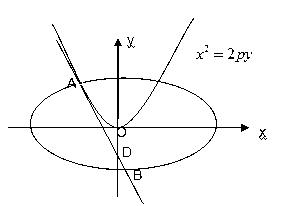
 的椭圆
的椭圆 恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,
恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k, ,①试用斜率k表示
,①试用斜率k表示 ②当
②当 ,在y轴上截得线段长为2
,在y轴上截得线段长为2 .
. ,求圆P的方程.
,求圆P的方程.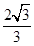 ).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点. 的焦点为
的焦点为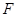 ,点
,点 ,线段
,线段 的中点在抛物线上. 设动直线
的中点在抛物线上. 设动直线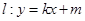 与抛物线相切于点
与抛物线相切于点 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以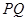 为直径的圆记为圆
为直径的圆记为圆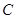 .
. 的值;
的值; 轴必有公共点;
轴必有公共点; ,使得圆
,使得圆 的圆心在坐标原点O,且恰好与直线
的圆心在坐标原点O,且恰好与直线 相切.
相切.
 轴于N,若动点Q满足
轴于N,若动点Q满足 (其中m为非零常数),试求动点
(其中m为非零常数),试求动点 的轨迹方程
的轨迹方程 .
. 时,得到动点Q的轨迹曲线C,与
时,得到动点Q的轨迹曲线C,与 垂直的直线
垂直的直线 与曲线C交于 B、D两点,求
与曲线C交于 B、D两点,求 面积的最大值.
面积的最大值. |=|
|=| |?若存在,求出D点的坐标;若不存在,说明理由.
|?若存在,求出D点的坐标;若不存在,说明理由.