题目内容
定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是 ,且当x∈
,且当x∈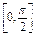 时,f(x)=sinx.
时,f(x)=sinx.
(1)求当x∈[- ,0]时,f(x)的解析式;
,0]时,f(x)的解析式;
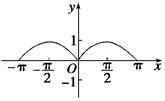
(2)画出函数f(x)在[- ,
, ]上的函数简图;
]上的函数简图;
(3)求当f(x)≥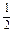 时,x的取值范围.
时,x的取值范围.
 ,且当x∈
,且当x∈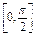 时,f(x)=sinx.
时,f(x)=sinx.(1)求当x∈[-
 ,0]时,f(x)的解析式;
,0]时,f(x)的解析式;(2)画出函数f(x)在[-
 ,
, ]上的函数简图;
]上的函数简图;(3)求当f(x)≥
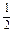 时,x的取值范围.
时,x的取值范围.(1)f(x)=-sinx(2)见解析(3)当x∈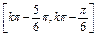 ,k∈Z时,f(x)≥
,k∈Z时,f(x)≥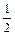
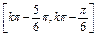 ,k∈Z时,f(x)≥
,k∈Z时,f(x)≥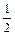
(1)∵f(x)是偶函数,∴f(-x)=f(x).
而当x∈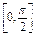 时,f(x)=sinx.∴当x∈
时,f(x)=sinx.∴当x∈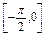 时,
时,
f(x)=f(-x)=sin(-x)=-sinx.
又当x∈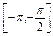 时,x+
时,x+ ∈
∈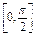 ,
,
∵f(x)的周期为 ,∴f(x)=f(
,∴f(x)=f( +x)=sin(
+x)=sin( +x)=-sinx.
+x)=-sinx.
∴当x∈[- ,0]时,f(x)=-sinx.
,0]时,f(x)=-sinx.
(2)如图:
(3)由于f(x)的最小正周期为 ,
,
因此先在[- ,0]上来研究f(x)≥
,0]上来研究f(x)≥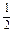 ,
,
即-sinx≥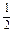 ,∴sinx≤-
,∴sinx≤-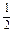 ,∴-
,∴-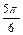 ≤x≤-
≤x≤-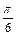 .
.
由周期性知,
当x∈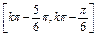 ,k∈Z时,f(x)≥
,k∈Z时,f(x)≥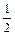 .
.

而当x∈
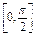 时,f(x)=sinx.∴当x∈
时,f(x)=sinx.∴当x∈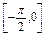 时,
时,f(x)=f(-x)=sin(-x)=-sinx.
又当x∈
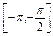 时,x+
时,x+ ∈
∈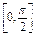 ,
,∵f(x)的周期为
 ,∴f(x)=f(
,∴f(x)=f( +x)=sin(
+x)=sin( +x)=-sinx.
+x)=-sinx.∴当x∈[-
 ,0]时,f(x)=-sinx.
,0]时,f(x)=-sinx.(2)如图:
(3)由于f(x)的最小正周期为
 ,
,因此先在[-
 ,0]上来研究f(x)≥
,0]上来研究f(x)≥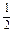 ,
,即-sinx≥
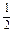 ,∴sinx≤-
,∴sinx≤-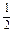 ,∴-
,∴-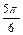 ≤x≤-
≤x≤-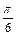 .
.由周期性知,
当x∈
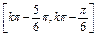 ,k∈Z时,f(x)≥
,k∈Z时,f(x)≥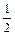 .
.
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
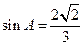 ,AD是BC边上的高,AD=
,AD是BC边上的高,AD=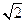 ,BC=2.
,BC=2.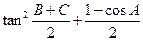 的值
的值 的函数解析式;
的函数解析式; 和
和 ,在B处测得C在前方,D在后方,且D处俯角为
,在B处测得C在前方,D在后方,且D处俯角为 ,
, 为
为
 ,
, ,求C、D的距离(结果用根式表示)
,求C、D的距离(结果用根式表示) 
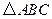 中,已知
中,已知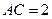 ,
,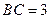 ,
,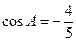 .
. (1)求
(1)求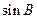 的值; (2)求
的值; (2)求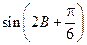 的值.
的值. 点发现乙船在北偏东60度的
点发现乙船在北偏东60度的 点处,测得乙船以每小时
点处,测得乙船以每小时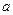 海里的速度向正北行驶,
海里的速度向正北行驶, 海里,则甲船如何航行才能最快地与乙船相遇?
海里,则甲船如何航行才能最快地与乙船相遇?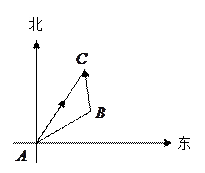

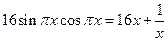 的解集合为 。
的解集合为 。 ,且
,且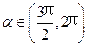 ,求
,求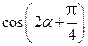 的值.
的值.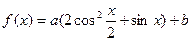 。
。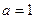 时,求
时,求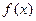 的单调递增区间:
的单调递增区间: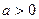 ,且
,且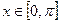 时,
时,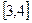 ,求
,求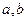 的值。
的值。