题目内容
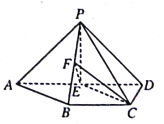
【题目】四棱锥
中，已知
平面PAD，
，
，E为棱PC上的一点，经过A，B，E三点的平面与棱PD相交于点F．
求证：
平面PAD；
求证：
；
若平面
平面PCD，求证：
．
【答案】（1）见解析；（2）见解析；（3）见解析
【解析】
推导出
，
，从而
平面ABCD，进而
，由
，能证明
平面PAD．
由平面PAD，
平面PAD，得
，从而
平面ABEF，由此能证明
．
由，，
，得到
平面ABE，由此能证明
．
平面PAD，
平面PAD，
，又，
，
平面ABCD，
平面ABCD，
，
，
，
平面PAD．
由知平面PAD，
又平面PAD，
，
平面ABEF，
平面ABEF，
平面ABEF，
平面PCD，平面
平面
，
．
由知，
平面PAD，，
又，
，
平面
平面PCD，平面
平面
，
平面PCD，
平面ABE，
又
平面ABE，
．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某市环保部门为了让全市居民认识到冬天烧煤取暖对空气
数值的影响，进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数
与空气数值不合格的天数
进行统计分析，得出下表数据：
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
（1）以统计数据为依据，求出关于的线性回归方程
；
（2）根据（1）求出的线性回归方程，预测该市烧煤取暖的天数为20时空气数值不合格的天数．
参考公式：
，
．
