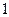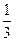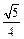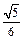题目内容
. (本小题满分9分)
(如图)在底面为平行四边形的四棱锥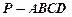 中,
中,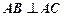 ,
,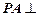 平面
平面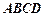 ,且
,且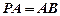 ,点
,点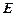 是
是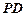 的中点.
的中点.
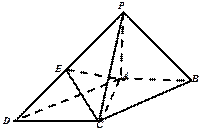
(Ⅰ)求证: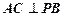 ;
;
(Ⅱ)求证: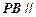 平面
平面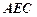 ;
;
(Ⅲ)(理科学生做)求二面角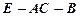 的大小.
的大小.
(文科学生做)当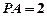 ,
,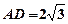 时,求直线
时,求直线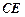 和平面
和平面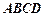 所成的线面角的大小.
所成的线面角的大小.
(如图)在底面为平行四边形的四棱锥
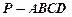 中,
中,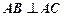 ,
,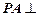 平面
平面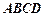 ,且
,且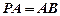 ,点
,点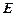 是
是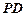 的中点.
的中点.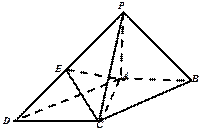
(Ⅰ)求证:
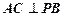 ;
;(Ⅱ)求证:
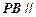 平面
平面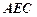 ;
;(Ⅲ)(理科学生做)求二面角
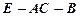 的大小.
的大小.(文科学生做)当
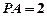 ,
,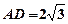 时,求直线
时,求直线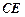 和平面
和平面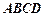 所成的线面角的大小.
所成的线面角的大小. 解:(Ⅰ)由
解:(Ⅰ)由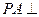 平面
平面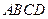 ,
,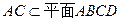 ,可得PA^AC
,可得PA^AC又
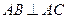 ,又
,又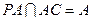 所以AC^平面PAB,所以
所以AC^平面PAB,所以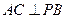 ……………3分
……………3分(Ⅱ)如图,连BD交AC于点O,连EO,则
EO是△PDB的中位线,\EO
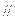 PB
PB 又PB
 平面
平面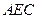 ,BO
,BO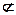 平面
平面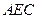
\PB
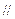 平面
平面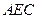 …………………………3分
…………………………3分(Ⅲ)(理)如图,取A
 D的中点F,连EF,FO,则EF是△PAD的中位线,\EF
D的中点F,连EF,FO,则EF是△PAD的中位线,\EF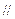 PA又
PA又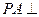 平面
平面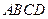 ,\EF^平面
,\EF^平面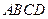
同理FO是△ADC的中位线,\FO
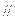 AB\FO^AC,可知\ÐEOF是二面角E-AC-D的平面角.又FO=
AB\FO^AC,可知\ÐEOF是二面角E-AC-D的平面角.又FO=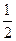 AB=
AB=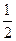 PA=EF\ÐEOF=45°而二面角
PA=EF\ÐEOF=45°而二面角 与二面角E-AC-D互补,
与二面角E-AC-D互补,故所求二面角
 的大小为135°………
的大小为135°……… ……3分
……3分(文)如图,取AD的中点F,连EF,FO,则EF是△PAD的中位线,
\EF
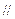 PA又
PA又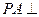 平面
平面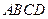 ,
,\EF^平面
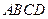 ,
,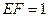 .连结
.连结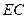 ,则
,则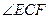 即为
即为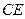 和平面
和平面 所成的线面角.
所成的线面角.在
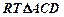 中,
中,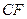 为斜边中线,所以
为斜边中线,所以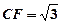 ,所以
,所以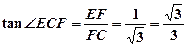 .
.故,
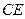 和平面
和平面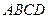 所成的线面角为
所成的线面角为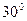 .……………3分
.……………3分略

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 分10分)
分10分) B1C1D1中,AA1 =
B1C1D1中,AA1 =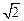 ,AB = 1,E是DD1的中点.
,AB = 1,E是DD1的中点.
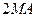 =
=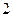

 所在平面与圆
所在平面与圆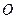 所在平面相交于
所在平面相交于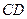 ,线段
,线段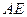 垂直于圆
垂直于圆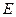 是圆
是圆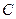 、
、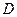 的点,
的点,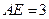 ,圆
,圆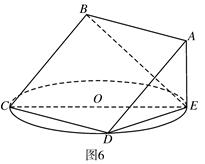
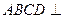 平面
平面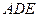 ;
;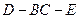 的平面角的正切值。
的平面角的正切值。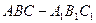 中,
中,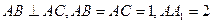 ,
,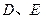 分别是
分别是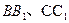 的中点,
的中点,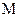 是
是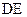 的中点.
的中点. 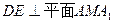 ;(2)求三棱锥
;(2)求三棱锥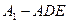 的体积;(3)求二面角
的体积;(3)求二面角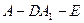 的余弦值.
的余弦值.
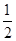
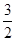

 线垂直
线垂直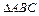 中,AB=2,BC=1,
中,AB=2,BC=1,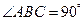 ,平面ABC外一点
,平面ABC外一点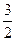 ,则三棱锥P—ABC的体积是( )
,则三棱锥P—ABC的体积是( )