题目内容
已知{an}为递增的等比数列,且{a1,a3,a5}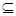 {-10,-6,-2,0,1,3,4,16}.
{-10,-6,-2,0,1,3,4,16}.
(1)求数列{an}的通项公式;
(2)是否存在等差数列{bn},使得a1bn+a2bn-1+a3bn-2+…+anb1=2n+1-n-2对一切n∈N*都成立?若存在,求出bn;若不存在,说明理由.
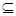 {-10,-6,-2,0,1,3,4,16}.
{-10,-6,-2,0,1,3,4,16}.(1)求数列{an}的通项公式;
(2)是否存在等差数列{bn},使得a1bn+a2bn-1+a3bn-2+…+anb1=2n+1-n-2对一切n∈N*都成立?若存在,求出bn;若不存在,说明理由.
(1) an=2n-1, (2) bn=n,
(1)由等比数列递增的性质得其首项为1,公比为4,可得到通项公式;(2)先由数列的前两项满足等式,求出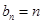 ;再写出
;再写出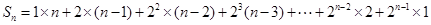 ,错位相减求出
,错位相减求出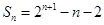 。即证出存在数列{bn},结论成立
。即证出存在数列{bn},结论成立
(1)因为{an}是递增的等比数列,所以数列{an}的公比是正数,
又{a1,a3,a5}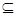 {-10,-6,-2,0,1,3,4,16},所以a1=1,a3=4,a5=16,
{-10,-6,-2,0,1,3,4,16},所以a1=1,a3=4,a5=16,
从而q2=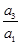 =4,q=2,an=a1qn-1=2n-1,所以数列{an}的通项公式为an=2n-1,
=4,q=2,an=a1qn-1=2n-1,所以数列{an}的通项公式为an=2n-1,
(2)假设存在满足条件的等差数列{bn},其公差为d.则当n=1时,a1b1=1,
又∵a1=1,∴b1=1;
当n=2时,a1b2+a2b1=4,b2+2b1=4,b2=2.
则d=b2-b1=1,∴bn=b1+(n-1)d=1+(n-1)×1=n.
以下证明当bn=n时,a1bn+a2bn-1+…+an-1b2+anb1=2n+1-n-2对一切n∈N*都成立.
设Sn=a1bn+a2bn-1+…+an-1b2+anb1,
即Sn=1×n+2×(n-1)+22×(n-2)+23×(n-3)+…+2n-2×2+2n-1×1, ①
2Sn=2×n+22×(n-1)+23×(n-2)+…+2n-1×2+2n×1, ②
②-①得Sn=-n+2+22+23+…+2n-1+2n=-n+ =2n+1-n-2,
=2n+1-n-2,
所以存在等差数列{bn},bn=n,使得a1bn+a2bn-1+…+an-1b2+anb1=2n+1-n-2对一切n∈N*都成立.
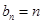 ;再写出
;再写出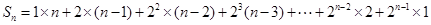 ,错位相减求出
,错位相减求出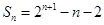 。即证出存在数列{bn},结论成立
。即证出存在数列{bn},结论成立(1)因为{an}是递增的等比数列,所以数列{an}的公比是正数,
又{a1,a3,a5}
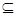 {-10,-6,-2,0,1,3,4,16},所以a1=1,a3=4,a5=16,
{-10,-6,-2,0,1,3,4,16},所以a1=1,a3=4,a5=16,从而q2=
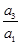 =4,q=2,an=a1qn-1=2n-1,所以数列{an}的通项公式为an=2n-1,
=4,q=2,an=a1qn-1=2n-1,所以数列{an}的通项公式为an=2n-1,(2)假设存在满足条件的等差数列{bn},其公差为d.则当n=1时,a1b1=1,
又∵a1=1,∴b1=1;
当n=2时,a1b2+a2b1=4,b2+2b1=4,b2=2.
则d=b2-b1=1,∴bn=b1+(n-1)d=1+(n-1)×1=n.
以下证明当bn=n时,a1bn+a2bn-1+…+an-1b2+anb1=2n+1-n-2对一切n∈N*都成立.
设Sn=a1bn+a2bn-1+…+an-1b2+anb1,
即Sn=1×n+2×(n-1)+22×(n-2)+23×(n-3)+…+2n-2×2+2n-1×1, ①
2Sn=2×n+22×(n-1)+23×(n-2)+…+2n-1×2+2n×1, ②
②-①得Sn=-n+2+22+23+…+2n-1+2n=-n+
 =2n+1-n-2,
=2n+1-n-2,所以存在等差数列{bn},bn=n,使得a1bn+a2bn-1+…+an-1b2+anb1=2n+1-n-2对一切n∈N*都成立.

练习册系列答案
相关题目
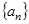 的前
的前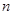 项和
项和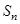 满足
满足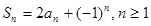 .
.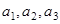 ;
;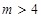 ,有
,有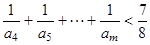 .
.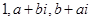 是一等比数列的连续三项,则a,b的值为( )
是一等比数列的连续三项,则a,b的值为( )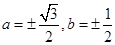
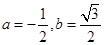
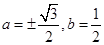

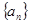 是首项为1的等比数列,
是首项为1的等比数列,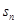 是
是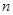 项和,且
项和,且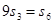 ,则数列
,则数列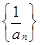 的前5项和为
的前5项和为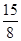 或5
或5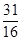 或5
或5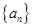 为等比数列,
为等比数列,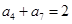 ,
,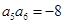 ,则
,则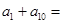 ( )
( )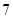
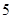
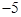
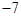
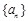 中,
中,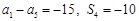 ,则
,则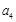 等于( )
等于( )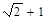 与
与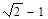 ,两数的等比中项是( )
,两数的等比中项是( )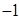
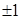
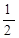
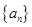 的前
的前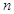 项为
项为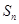 ,
,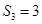 ,
,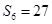 ,则此等比数列的公比
,则此等比数列的公比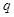 等于______
等于______