题目内容
已知数列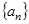 的前
的前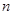 项和
项和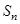 满足
满足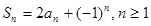 .
.
(1)写出数列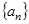 的前三项
的前三项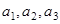 ;
;
(2)求数列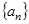 的通项公式;
的通项公式;
(3)证明:对任意的整数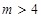 ,有
,有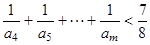 .
.
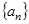 的前
的前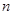 项和
项和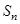 满足
满足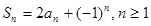 .
.(1)写出数列
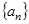 的前三项
的前三项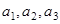 ;
;(2)求数列
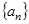 的通项公式;
的通项公式;(3)证明:对任意的整数
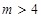 ,有
,有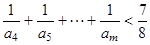 .
.(1) 由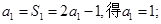 由
由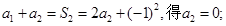
由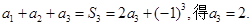
(2)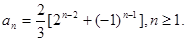
(3)见解析.
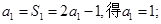 由
由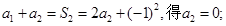
由
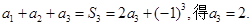
(2)
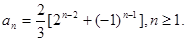
(3)见解析.
.
(1)因为数列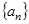 的前
的前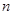 项和
项和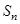 满足
满足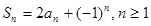 ,那么对于n令值,边可以写出数列
,那么对于n令值,边可以写出数列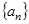 的前三项
的前三项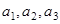 ;
;
(2)根据前几项归纳猜想数列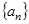 的通项公式;再用数学归纳法加以证明。或者里利用迭代思想
的通项公式;再用数学归纳法加以证明。或者里利用迭代思想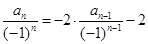 ,得到通项公式。
,得到通项公式。
(3)利用放缩法得到求和,并证明不等式。
(1)为了计算前三项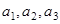 的值,只要在递推式
的值,只要在递推式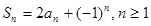 中,对
中,对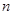 取特殊值
取特殊值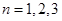 ,就可以消除解题目标与题设条件之间的差异.
,就可以消除解题目标与题设条件之间的差异.
由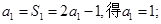
由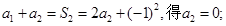
由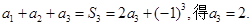
(2)为了求出通项公式,应先消除条件式中的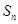 .事实上
.事实上
当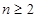 时,有
时,有
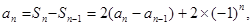
即有
从而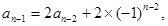
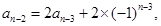
……
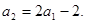
接下来,逐步迭代就有
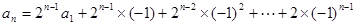
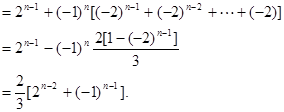
经验证a1也满足上式,故知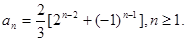
其实,将关系式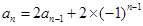 和课本习题
和课本习题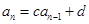 作联系,容易想到:这种差异的消除,只要对
作联系,容易想到:这种差异的消除,只要对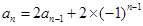 的两边同除以
的两边同除以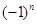 ,便得
,便得
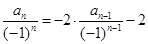 .
.
令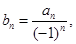 就有
就有
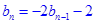 ,
,
于是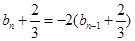 ,
,
这说明数列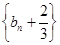 是等比数列,公比
是等比数列,公比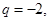 首项
首项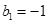 ,从而,得
,从而,得
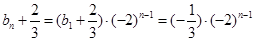 ,
,
即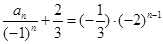 ,
,
故有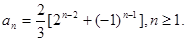
(3)由通项公式得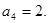
当 且n为奇数时,
且n为奇数时, 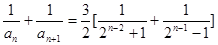
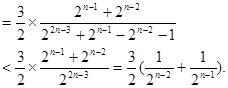
当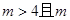 为偶数时,
为偶数时,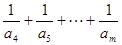
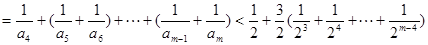
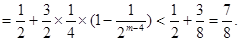
当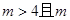 为奇数时,
为奇数时,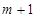 为偶数,可以转化为上面的情景
为偶数,可以转化为上面的情景
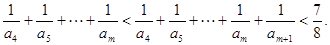
故任意整数m>4,有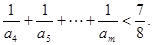
(1)因为数列
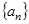 的前
的前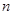 项和
项和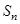 满足
满足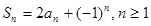 ,那么对于n令值,边可以写出数列
,那么对于n令值,边可以写出数列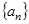 的前三项
的前三项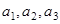 ;
;(2)根据前几项归纳猜想数列
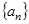 的通项公式;再用数学归纳法加以证明。或者里利用迭代思想
的通项公式;再用数学归纳法加以证明。或者里利用迭代思想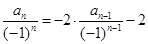 ,得到通项公式。
,得到通项公式。(3)利用放缩法得到求和,并证明不等式。
(1)为了计算前三项
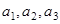 的值,只要在递推式
的值,只要在递推式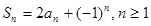 中,对
中,对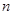 取特殊值
取特殊值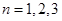 ,就可以消除解题目标与题设条件之间的差异.
,就可以消除解题目标与题设条件之间的差异.由
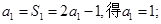
由
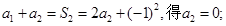
由
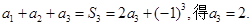
(2)为了求出通项公式,应先消除条件式中的
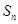 .事实上
.事实上当
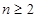 时,有
时,有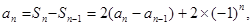
即有

从而
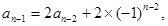
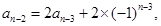
……
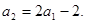
接下来,逐步迭代就有
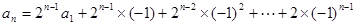
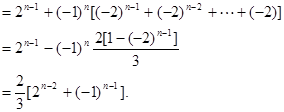
经验证a1也满足上式,故知
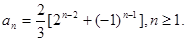
其实,将关系式
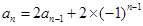 和课本习题
和课本习题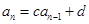 作联系,容易想到:这种差异的消除,只要对
作联系,容易想到:这种差异的消除,只要对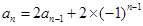 的两边同除以
的两边同除以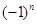 ,便得
,便得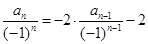 .
.令
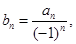 就有
就有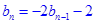 ,
,于是
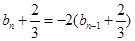 ,
,这说明数列
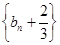 是等比数列,公比
是等比数列,公比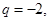 首项
首项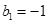 ,从而,得
,从而,得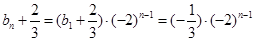 ,
,即
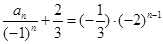 ,
,故有
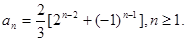
(3)由通项公式得
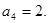
当
 且n为奇数时,
且n为奇数时, 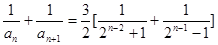
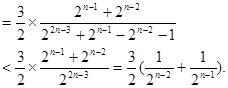
当
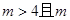 为偶数时,
为偶数时,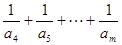
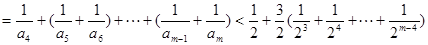
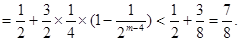
当
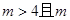 为奇数时,
为奇数时,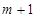 为偶数,可以转化为上面的情景
为偶数,可以转化为上面的情景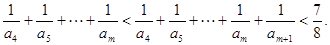
故任意整数m>4,有
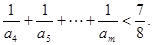

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
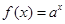 (
(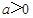 且
且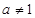 )的图象上,等比数列
)的图象上,等比数列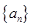 的前
的前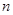 项和为
项和为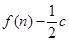 ,数列
,数列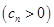 的首项为c,且其前
的首项为c,且其前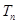 满足 2
满足 2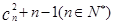 .
.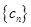 的通项公式;
的通项公式;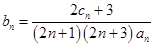 ,求数列
,求数列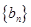 的前
的前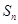 .
. 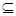 {-10,-6,-2,0,1,3,4,16}.
{-10,-6,-2,0,1,3,4,16}.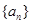 ,已知
,已知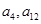 是方程
是方程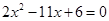 的两根,则
的两根,则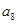 等于( )
等于( )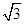
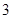
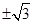
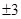
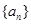 的公比
的公比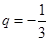 ,则
,则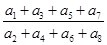 等于( )
等于( )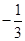
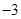
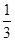
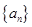 中,
中,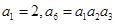 ,则公比
,则公比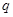 的值为( )
的值为( ) 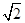


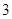
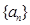 前
前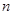 项的和为
项的和为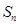 , 且
, 且 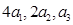 成等差数列,若
成等差数列,若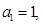 则
则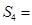
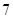
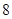
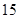
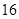
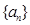 中,
中,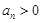 ,且
,且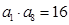 ,则
,则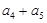 的最小值为______.
的最小值为______.