题目内容
设函数f(x)＝sin(ωx＋φ)＋cos(ωx＋φ)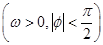
的最小正周期为π，且f(－x)＝f(x)，则( )
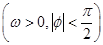的最小正周期为π，且f(－x)＝f(x)，则( )A．y＝f(x)在 上单调递减 |
B．y＝f(x)在 上单调递减 |
C．y＝f(x)在 上单调递增 |
| D．y＝f(x)在上单调递增 |
A
变形f(x)＝sin(ωx＋φ)＋cos(ωx＋φ)
＝
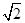sin
．
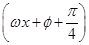又f(－x)＝f(x)，得函数为偶函数，故φ＋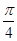
＝kπ＋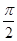
(k∈Z)．
∴φ＝kπ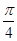＋(k∈Z)．
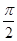∵|φ|<，∴φ＝．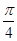
又T＝π，∴ω＝2．
∴f(x)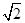＝sin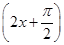
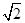＝cos 2x．
结合图象知A正确．
＝
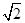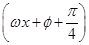sin．又f(－x)＝f(x)，得函数为偶函数，故φ＋
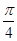＝kπ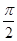＋(k∈Z)．∴φ＝kπ＋
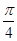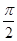(k∈Z)．∵|φ|<
，∴φ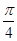＝．又T＝π，∴ω＝2．
∴f(x)＝
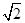sin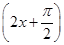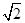＝cos 2x．结合图象知A正确．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
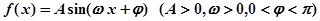的部分图象，如图所示．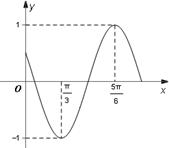
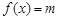在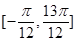
有两个不同的实根，求
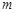的取值范围．
)+
是奇函数，且在[0，
]上是减函数的
，则函数
的图像（ ）
对称
对称
对称
对称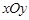
中，直线
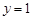与函数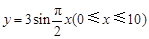
的图象所有交点的横坐标之和为 ．
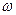x+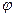
)(
<
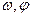的值分别是（ ）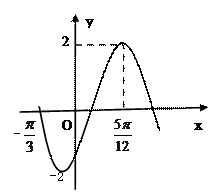
（ ）
上递增
上递增，在
上递减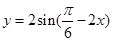 
(
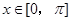)为增函数的区间是( )
sin3x+cos3x，若对任意实数x都有|f（x）|≤a，则实数a的取值范围是 .