题目内容
已知圆C1的方程为x2+y2+4x-5=0,圆C2的方程为x2+y2-4x+3=0,动圆C与圆C1、C2相外切.(I)求动圆C圆心轨迹E的方程;
(II)若直线l过点(2,0)且与轨迹E交于P、Q两点.
①设点M(m,0),问:是否存在实数m,使得直线l绕点(2,0)无论怎样转动,都有
 •
•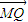 =0成立?若存在,求出实数m的值;若不存在,请说明理由;
=0成立?若存在,求出实数m的值;若不存在,请说明理由;②过P、Q作直线x=
 的垂线PA、QB,垂足分别为A、B,记λ=
的垂线PA、QB,垂足分别为A、B,记λ=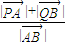 ,求λ,的取值范围.
,求λ,的取值范围.
【答案】分析:(I)|CC1|-|CC2|=r1-r2=2,圆心C的轨迹E是以C1、C2为焦点的双曲线右支,由c=2,2a=2,知b2=3,由此能注出轨迹E的方程.
(II)当直线l的斜率存在时,设直线l的方程为y=k(x-2),与双曲线方程联立消y得(k2-3)x2-4k2x+3=0,设P(x1,y1),Q(x2,y2),解得k2>3.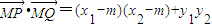 =
=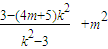 .
.
①假设存在实数m,使得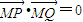 ,故得2(1-m2)+k2(m2-4m-5)=0,对任意的k2>3恒成立,解得m=-1.由此能够导出存在m=-1,使得
,故得2(1-m2)+k2(m2-4m-5)=0,对任意的k2>3恒成立,解得m=-1.由此能够导出存在m=-1,使得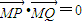 .
.
②由a=1,c=2,知直线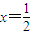 是双曲线的右准线,所以
是双曲线的右准线,所以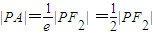 ,|QB|=
,|QB|= |QF2|,
|QF2|,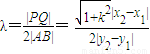 =
=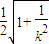 ,由k2>3,知
,由k2>3,知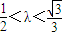 .当斜率不存在时,
.当斜率不存在时,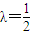 .由此能求出λ的取值范围.
.由此能求出λ的取值范围.
解答:解:(I)圆C1的圆心C1(-2,0),半径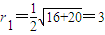 ,
,
圆C2的圆心C2(2,0),半径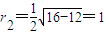 ,
,
|CC1|-|CC2|=r1-r2=2,
圆心C的轨迹E是以C1、C2为焦点的双曲线右支,由c=2,2a=2,
∴b2=3,
故轨迹E的方程为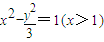 .…(4分)
.…(4分)
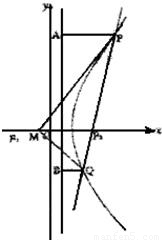 (II)当直线l的斜率存在时,设直线l的方程为y=k(x-2),
(II)当直线l的斜率存在时,设直线l的方程为y=k(x-2),
与双曲线方程联立消y得
(k2-3)x2-4k2x+3=0,
设P(x1,y1),Q(x2,y2),
∴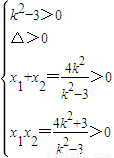 ,
,
解得k2>3.
∵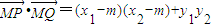
=(x1-m)(x2-m)+k2(x1-2)(x2-2)
=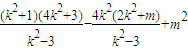 +4k2
+4k2
=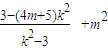 .
.
①假设存在实数m,使得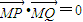 ,故得
,故得
2(1-m2)+k2(m2-4m-5)=0,
对任意的k2>3恒成立,
∴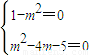 ,
,
解得m=-1.
∴当m=-1时,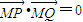 .
.
当直线l的斜率不存在时,由P(2,3),Q(2,-3)及M(1,0)知结论也成立.
综上所述,存在m=-1,使得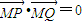 .
.
②∵a=1,c=2,
∴直线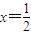 是双曲线的右准线,
是双曲线的右准线,
∴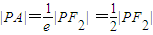 ,|QB|=
,|QB|= |QF2|,
|QF2|,
∴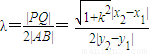
=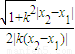
=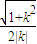
=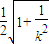 ,
,
∵k2>3,
∴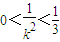 ,
,
∴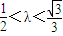 .
.
当斜率不存在时,|PQ|=|AB|,此时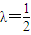 .
.
故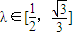 .
.
点评:本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.
(II)当直线l的斜率存在时,设直线l的方程为y=k(x-2),与双曲线方程联立消y得(k2-3)x2-4k2x+3=0,设P(x1,y1),Q(x2,y2),解得k2>3.
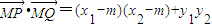 =
=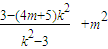 .
.①假设存在实数m,使得
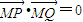 ,故得2(1-m2)+k2(m2-4m-5)=0,对任意的k2>3恒成立,解得m=-1.由此能够导出存在m=-1,使得
,故得2(1-m2)+k2(m2-4m-5)=0,对任意的k2>3恒成立,解得m=-1.由此能够导出存在m=-1,使得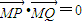 .
.②由a=1,c=2,知直线
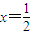 是双曲线的右准线,所以
是双曲线的右准线,所以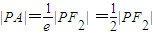 ,|QB|=
,|QB|= |QF2|,
|QF2|,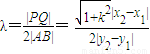 =
=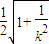 ,由k2>3,知
,由k2>3,知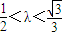 .当斜率不存在时,
.当斜率不存在时,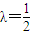 .由此能求出λ的取值范围.
.由此能求出λ的取值范围.解答:解:(I)圆C1的圆心C1(-2,0),半径
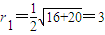 ,
,圆C2的圆心C2(2,0),半径
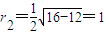 ,
,|CC1|-|CC2|=r1-r2=2,
圆心C的轨迹E是以C1、C2为焦点的双曲线右支,由c=2,2a=2,
∴b2=3,
故轨迹E的方程为
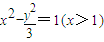 .…(4分)
.…(4分) (II)当直线l的斜率存在时,设直线l的方程为y=k(x-2),
(II)当直线l的斜率存在时,设直线l的方程为y=k(x-2),与双曲线方程联立消y得
(k2-3)x2-4k2x+3=0,
设P(x1,y1),Q(x2,y2),
∴
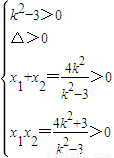 ,
,解得k2>3.
∵
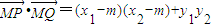
=(x1-m)(x2-m)+k2(x1-2)(x2-2)
=
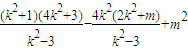 +4k2
+4k2=
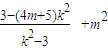 .
.①假设存在实数m,使得
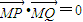 ,故得
,故得2(1-m2)+k2(m2-4m-5)=0,
对任意的k2>3恒成立,
∴
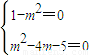 ,
,解得m=-1.
∴当m=-1时,
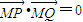 .
.当直线l的斜率不存在时,由P(2,3),Q(2,-3)及M(1,0)知结论也成立.
综上所述,存在m=-1,使得
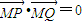 .
.②∵a=1,c=2,
∴直线
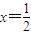 是双曲线的右准线,
是双曲线的右准线,∴
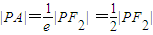 ,|QB|=
,|QB|= |QF2|,
|QF2|,∴
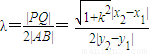
=
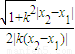
=
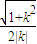
=
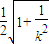 ,
,∵k2>3,
∴
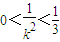 ,
,∴
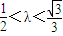 .
.当斜率不存在时,|PQ|=|AB|,此时
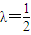 .
.故
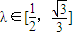 .
.点评:本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
相关题目
 如图,已知圆C1的方程为
如图,已知圆C1的方程为 ,椭圆C2的方程为
,椭圆C2的方程为 ,C2的离心率为
,C2的离心率为 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求:
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求: ,椭圆C2的方程为
,椭圆C2的方程为 ,C2的离心率为
,C2的离心率为 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求:
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求: