Question

(本小题满分12分)
已知圆C₁的方程为(x－2)²+(y－1)²=，椭圆C₂的方程为，C₂的离心率为，如果C₁与C₂相交于A、B两点，且线段AB恰为圆C₁的直径，试求：
（1）直线AB的方程；（2）椭圆C₂的方程.

Answer 1

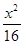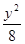（1）y= －x+3；（2）+=1。

解析试题分析：（1）由e=，得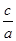=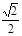，a²=2c²,b²=c²。
设椭圆方程为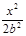+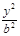=1。又设A(x₁,y₁),B(x₂,y₂)。由圆心为(2,1)，得x₁+x₂=4,y₁+y₂=2。
又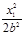+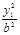=1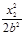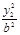，+=1，两式相减，得 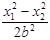+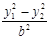=0。
∴
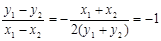
∴直线AB的方程为y－1= －(x－2)，即y= －x+3。
（2）将y= －x+3代入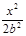+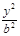=1，得3x²－12x+18－2b²=0
又直线AB与椭圆C₂相交，∴Δ=24b²－72>0。
由|AB|=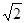|x₁－x₂|=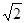=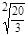,得·=。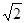
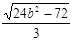解得  b²=8，故所求椭圆方程为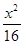+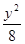=1。
考点：本题考查椭圆的简单性质；圆与椭圆的综合应用。
点评：一般情况下，遇到弦中点的问题可以优先考虑点差法。利用点差法可以减少很多的计算，因此在解有关的问题时用这种方法比较好。点差法适应的常见问题：弦的斜率与弦的中点问题。