题目内容
【题目】我们称满足以下两个条件的有穷数列![]() 为
为![]() 阶“期待数列”;①
阶“期待数列”;①![]() ;②
;②![]() .
.
(1)若数列![]() 的通项公式是
的通项公式是![]() ,试判断数列
,试判断数列![]() 是否为2014阶“期待数列”,并说明理由;
是否为2014阶“期待数列”,并说明理由;
(2)若等比数列![]() 为
为![]() 阶“期待数列”,求公比
阶“期待数列”,求公比![]() 及数列
及数列![]() 的通项公式;
的通项公式;
(3)若一个等差数列![]() 既是(
既是(![]() )阶“期待数列”又是递增数列,求该数列的通项公式.
)阶“期待数列”又是递增数列,求该数列的通项公式.
【答案】(1)是;(2)![]() ,
,![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)由通项公式,利用分组求和法可证明![]() ;
;![]() ;从而可得结论;(2)先证明
;从而可得结论;(2)先证明![]() ,由①
,由①![]() ,得
,得![]() ,由②得
,由②得![]() 或
或![]() ,利用等比数列的通项公式可得结果;(3)设等差数列
,利用等比数列的通项公式可得结果;(3)设等差数列![]() 的公差为
的公差为![]() ,
,![]() ,根据
,根据![]() 既是(
既是(![]() )阶“期待数列”,求出首项与公差,利用等差数列的通项公式可得结果.
)阶“期待数列”,求出首项与公差,利用等差数列的通项公式可得结果.
(1)∵![]() ,
,
所以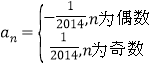 ,
,
∴![]()
![]() ,
,
![]() ,
,
所以数列![]() 为2014阶“期待数列”;
为2014阶“期待数列”;
(2)若![]() ,由①得,
,由①得,![]() ,得
,得![]() ,矛盾
,矛盾
若![]() ,则由①
,则由①![]() ,得
,得![]() ,由②得
,由②得![]() 或
或![]() ,
,
所以,![]() ,数列
,数列![]() 的通项公式为
的通项公式为![]() 或
或![]() ;
;
(3)设等差数列![]() 的公差为
的公差为![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∵![]() ,由
,由![]() ,得
,得![]() ,
,
由①、②知![]() ,两式相减得
,两式相减得![]() ,∴
,∴![]() ,
,
又![]() ,得
,得![]() ,
,
∴数列![]() 的通项公式是
的通项公式是![]() .
.

练习册系列答案
相关题目