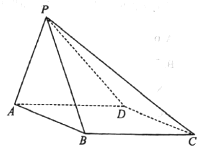
题目内容
【题目】已知抛物线![]() ,圆
,圆![]() .
.
(Ⅰ)![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是抛物线
是抛物线![]() 上的定点,
上的定点,![]() ,求抛物线
,求抛物线![]() 的方程;
的方程;
(Ⅱ)在(Ⅰ)的条件下,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切,设直线
相切,设直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,则在
两点,则在![]() 轴上是否存在点
轴上是否存在点![]() 使
使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;
;
(Ⅱ)见解析.
【解析】
(Ⅰ)由题,求得焦点F的坐标,再求得点A的坐标,代入求得方程;
(Ⅱ)先由题求得直线l的方程,再假设存在点![]() 使
使![]() ,转化为
,转化为![]() ,然后联立方程,求得斜率相加为0,解得M的坐标即可.
,然后联立方程,求得斜率相加为0,解得M的坐标即可.
(Ⅰ)抛物线C的焦点为![]() ,
,
由![]()
代入抛物线方程得p=2,故抛物线C的方程为:![]()
(Ⅱ)当直线的斜率不存在时,过点![]() 的直线不可能与圆E相切;
的直线不可能与圆E相切;
所以过抛物线焦点与圆相切的直线的斜率存在,
设直线斜率为k,则所求的直线方程为![]() ,
,
所以圆心到直线l的距离为![]()
当直线l与圆相切时,有
所以所求的切线方程为![]() 或
或![]()
不妨设直线l:![]() ,交抛物线于
,交抛物线于![]() 两点,
两点,
联立方程组 得
得![]() .
.
所以![]() ,,
,,
假设存在点![]() 使
使![]() ,则
,则![]() . 所以
. 所以

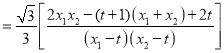

即t=-1故存在点![]() 符合条件
符合条件
当直线l:![]() 时,
时,
由对称性易知点![]() 也符合条件
也符合条件
综上存在点![]() 使
使![]()

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
【题目】某公司为了预测下月产品销售情况,找出了近7个月的产品销售量![]() (单位:万件)的统计表:
(单位:万件)的统计表:
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售量 |
|
|
|
|
|
|
|
但其中数据污损不清,经查证![]() ,
,![]() ,
, .
.
(1)请用相关系数说明销售量![]() 与月份代码
与月份代码![]() 有很强的线性相关关系;
有很强的线性相关关系;
(2)求![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)公司经营期间的广告宣传费![]() (单位:万元)(
(单位:万元)(![]() ),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
参考公式及数据:![]() ,相关系数
,相关系数 ,当
,当![]() 时认为两个变量有很强的线性相关关系,回归方程
时认为两个变量有很强的线性相关关系,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.