题目内容
【题目】已知数列![]() 是各项均为正数的等差数列.
是各项均为正数的等差数列.
(1)若![]() ,且
,且![]() 成等比数列,求数列
成等比数列,求数列![]() 的通项公式
的通项公式![]() ;
;
(2)在(1)的条件下,数列![]() 的前
的前![]() 和为
和为![]() ,设
,设![]() ,若对任意的
,若对任意的![]() ,不等式
,不等式![]() 恒成立,求突数
恒成立,求突数![]() 的最小值:
的最小值:
(3)若数列![]() 中有两项可以表示位某个整数
中有两项可以表示位某个整数![]() 的不同次冪,求证:数列
的不同次冪,求证:数列![]() 中存在无穷多项构成等比数列.
中存在无穷多项构成等比数列.
【答案】(1)![]() 的通项公式
的通项公式![]() .(2)实数
.(2)实数![]() 的最小值为
的最小值为![]() .
.
(3)有等比数列![]() ,其中
,其中![]() .
.
【解析】
本试题主要是考查了数列的通项公式和数列求和的综合运用。
(1)因为因为![]() 又因为
又因为![]() 是正项等差数列,故
是正项等差数列,故![]() ,利用等差数列的某两项可知其通项公式的求解。
,利用等差数列的某两项可知其通项公式的求解。
(2)因为![]() ,可知其
,可知其![]() 的通项公式,利用裂项求和的思想得到结论。
的通项公式,利用裂项求和的思想得到结论。
(3)因为这个数列的所有项都是正数,并且不相等,所以![]() ,
,
设![]() 其中
其中![]() 是数列的项,
是数列的项,![]() 是大于1的整数,
是大于1的整数,![]()
分析证明。
(1)因为![]() 又因为
又因为![]() 是正项等差数列,故
是正项等差数列,故![]()
所以![]() ,得
,得![]() 或
或![]() (舍去) ,
(舍去) ,
所以数列![]() 的通项公式
的通项公式![]() .………………………………………………4分
.………………………………………………4分
(2) 因为![]() ,
,
![]() ,
,
![]()
![]() ,
,
令![]() ,则
,则![]() , 当
, 当![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上是增函数,故当
上是增函数,故当![]() 时,
时,![]() ,即当
,即当![]() 时,
时,![]() , 要使对任意的正整数
, 要使对任意的正整数![]() , 不等式
, 不等式![]() 恒成立,
恒成立,
则须使![]() , 所以实数
, 所以实数![]() 的最小值为
的最小值为![]() .…………………………10分
.…………………………10分
(3)因为这个数列的所有项都是正数,并且不相等,所以![]() ,
,
设![]() 其中
其中![]() 是数列的项,
是数列的项,![]() 是大于1的整数,
是大于1的整数,![]() ,
,
令![]() ,则
,则![]() ,
,
故![]() 是
是![]() 的整数倍,对
的整数倍,对![]() 的
的![]() 次幂
次幂![]() ,
,
所以![]() ,右边是
,右边是![]() 的整数倍.
的整数倍.
所有![]() 这种形式是数列
这种形式是数列![]() 中某一项,
中某一项,
因此有等比数列![]() ,其中
,其中![]() . …………………………16分
. …………………………16分

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程![]() (
(![]() 精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
(Ⅱ)从表中的5天中任取一天,若已知所选取该天的热奶茶销售杯数大于120,求所选取该天热奶茶销售杯数大于130的概率.
参考数据:![]() ,
,![]() .参考公式:
.参考公式: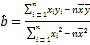 ,
,![]()

