题目内容
【题目】已知数列![]() 满足:
满足:![]() ,
,![]() ,且
,且![]() (n=1,2,...).记
(n=1,2,...).记
集合![]() .
.
(1)(Ⅰ)若![]() ,写出集合M的所有元素;
,写出集合M的所有元素;
(2)(Ⅱ)若集合M存在一个元素是3的倍数,证明:M的所有元素都是3的倍数;
(3)(Ⅲ)求集合M的元素个数的最大值.
【答案】
(1)
{6,12,24}
(2)
证明:(Ⅱ)因为集合M存在一个元素是3的倍数,所以不妨设 ak 是3的倍数,由已知 ![]() ,可用用数学归纳法证明对任意 n ≥ k , an 是3的倍数,当 k = 1 时,则M中的所有元素都是3的倍数,如果 k > 1 时,因为 ak = 2ak-1 或 2ak-1 -36 ,所以 2ak-1 是3的倍数,于是 ak-1 是3的倍数,类似可得, ak -2 . . . . . . a1 都是3的倍数,从而对任意 n ≥ 1 , an 是3的倍数,因此M的所有元素都是3的倍数.
,可用用数学归纳法证明对任意 n ≥ k , an 是3的倍数,当 k = 1 时,则M中的所有元素都是3的倍数,如果 k > 1 时,因为 ak = 2ak-1 或 2ak-1 -36 ,所以 2ak-1 是3的倍数,于是 ak-1 是3的倍数,类似可得, ak -2 . . . . . . a1 都是3的倍数,从而对任意 n ≥ 1 , an 是3的倍数,因此M的所有元素都是3的倍数.
(3)
8
【解析】(Ⅰ)由已知![]() 可知:
可知:![]() ,因此
,因此![]() 。
。
(Ⅱ)因为集合M存在一个元素是3的倍数,所以不妨设![]() 是3的倍数,由已知
是3的倍数,由已知![]() ,可用用数学归纳法证明对任意
,可用用数学归纳法证明对任意![]() ,
,![]() 是3的倍数,当
是3的倍数,当![]() 时,则M中的所有元素都是3的倍数,如果
时,则M中的所有元素都是3的倍数,如果![]() 时,因为
时,因为![]() 或
或![]() ,所以
,所以![]() 是3的倍数,于是
是3的倍数,于是![]() 是3的倍数,类似可得,
是3的倍数,类似可得,![]() 都是3的倍数,从而对任意
都是3的倍数,从而对任意![]() ,
,![]() 是3的倍数,因此M的所有元素都是3的倍数.
是3的倍数,因此M的所有元素都是3的倍数.
(III )由于M中的元素都不超过36,由![]() ,易得
,易得![]() ,类似可得
,类似可得![]() ,其次M中的元素个数最多除了前面两个数外,都是4的倍数,因为第二哥数必定为偶数,由
,其次M中的元素个数最多除了前面两个数外,都是4的倍数,因为第二哥数必定为偶数,由![]() 的定义可知,第三个数后面的数必定是4的倍数,另外,M中的数除以9的余数,由定义可知,
的定义可知,第三个数后面的数必定是4的倍数,另外,M中的数除以9的余数,由定义可知,![]() 和
和![]() 除以9的余数一样,
除以9的余数一样,
(1)若![]() 中有3的倍数,由(2)知:所有
中有3的倍数,由(2)知:所有![]() 都是3的倍数,所以
都是3的倍数,所以![]() 都是3的倍数,所以
都是3的倍数,所以![]() 除以9的余数为3,6,3,6,......,或6,3,6,3......,或0,0,0......,而除以9余3且是4的倍数只有12,除以9余6且是4的倍数只有24,除以9余0且是4的倍数只有36,则M中的数从第三项起最多2项,加上前面两项,最多4项。
除以9的余数为3,6,3,6,......,或6,3,6,3......,或0,0,0......,而除以9余3且是4的倍数只有12,除以9余6且是4的倍数只有24,除以9余0且是4的倍数只有36,则M中的数从第三项起最多2项,加上前面两项,最多4项。
(2)若![]() 中没有3的倍数,则
中没有3的倍数,则![]() 都不是3的倍数,对于
都不是3的倍数,对于![]() 除以9的余数只能是1,4,7,2,5,8中的一个,从
除以9的余数只能是1,4,7,2,5,8中的一个,从![]() 起,
起,![]() 除以9的余数是1,2,4,8,7,5,1,2,4,8,......,不断的6项循环(可能从2,4,8,7或5开始),而除以9的余数是1,2,4,8,5且是4的倍数(不大于36),只有28,20,4,8,16,32,所以M中的项加上前两项最多的8项,则
除以9的余数是1,2,4,8,7,5,1,2,4,8,......,不断的6项循环(可能从2,4,8,7或5开始),而除以9的余数是1,2,4,8,5且是4的倍数(不大于36),只有28,20,4,8,16,32,所以M中的项加上前两项最多的8项,则![]() 时,
时,![]() ,项数为8,所以集合M的元素个数的最大值为8.
,项数为8,所以集合M的元素个数的最大值为8.
【考点精析】根据题目的已知条件,利用数学归纳法的步骤的相关知识可以得到问题的答案,需要掌握
- 步骤:A.命题在n=1(或
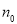 )时成立,这是递推的基础;B.假设在n=k时命题成立; C.证明n=k+1时命题也成立,完成这两步,就可以断定对任何自然数(或n>=
)时成立,这是递推的基础;B.假设在n=k时命题成立; C.证明n=k+1时命题也成立,完成这两步,就可以断定对任何自然数(或n>=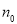 ,且
,且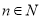 )结论都成立
)结论都成立
.


