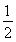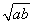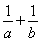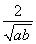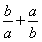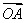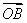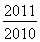题目内容
已知函数f(x)是定义在R上的奇函数，当x＜0时，f(x)＝ex(x＋1)，给出下列命题：
①当x＞0时，f(x)＝ex(1－x)；②函数f(x)有两个零点；③f(x)＞0的解集为(－1,0)∪(1，＋∞)；④?x1，x2∈R，都有|f(x1)－f(x2)|＜2.
其中正确命题的个数是( )
A．1 B．2
C．3 D．4
B
【解析】根据函数y＝f(x)是奇函数，当x＜0时，f(x)＝ex(x＋1)，可知x＞0时的解析式为f(x)＝－e－x(－x＋1)，①不正确；函数有三个零点，②不正确；命题③④成立．选B.
练习册系列答案
阳光课堂同步练习系列答案
相关题目
已知集合A、B，定义集合A与B的一种运算A⊕B，其结果如下表所示：
A | {1,2,3,4} | {－1,1} | {－4,8} | {－1,0,1} |
B | {2,3,6} | {－1,1} | {－4，－2,0,2} | {－2，－1,0,1} |
A⊕B | {1,4,6} | ∅ | {－2,0,2,8} | {－2} |
按照上述定义，若M＝{－2 011,0,2 012}，N＝{－2 012,0,2 013}，则M⊕N＝________.
