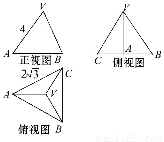
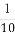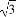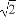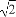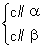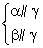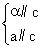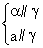题目内容
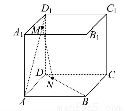
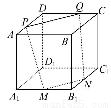
如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP= ,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ= .
,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ= .
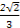 a
a
【解析】∵平面ABCD∥平面A1B1C1D1,∴MN∥PQ.
∵M,N分别是A1B1,B1C1的中点,AP= ,∴CQ=
,∴CQ= ,从而DP=DQ=
,从而DP=DQ=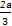 ,∴PQ=
,∴PQ=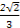 a.
a.
【误区警示】本题易忽视平面与平面平行的性质,不能正确找出Q点的位置,从而无法计算或计算出错,造成失分.

练习册系列答案
相关题目