Question

【题目】如图所示，P是△ABC所在平面外的一点，点A′，B′，C′分别是△PBC，△PCA，△PAB的重心．

(1)求证：平面ABC∥平面A′B′C′；

(2)求△A′B′C′与△ABC的面积之比．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）分别连接PA′，PB′，PC′并延长交BC，AC，AB于点D，E，F，连接DE，EF，DF．推导出A′C′∥DF．从而A′C′∥平面ABC．同理，A′B′∥平面ABC．由此能证明平面ABC∥平面A′B′C′；（2）推导出A′C′∥AC且A′C′=AC．A′B′∥AB且A′B′=AB，B′C′∥BC且B′C′=BC，由此能求出△A′B′C′与△ABC的面积之比．

(1)证明：分别连接PA′，PB′，PC′并延长交BC，AC，AB于点D，E，F，连接DE，EF，DF.

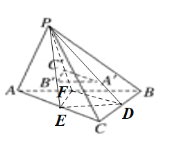
∵点A′，C′分别是△PBC，△PAB的重心，

∴PA′＝PD，PC′＝PF，

∴A′C′∥DF.

∵A′C′平面ABC，DF平面ABC，∴A′C′∥平面ABC.

同理，A′B′∥平面ABC.

又A′C′∩A′B′＝A′，A′C′，A′B′平面A′B′C′，

∴平面ABC∥平面A′B′C′.

(2)解　由(1)知A′C′∥DF且A′C′＝DF，

又DF∥AC且DF＝AC，

∴A′C′∥AC且A′C′＝AC.

同理，A′B′∥AB且A′B′＝AB，B′C′∥BC且B′C′＝BC，

∴△A′B′C′∽△ABC，

∴S△A′B′C′∶S△ABC＝1∶9.