题目内容
设向量a=(2,sinθ),b=(1,cosθ),θ为锐角(1)若a·b=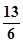 ,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+
,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+ )的值.
)的值.
(1)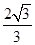 (2)
(2)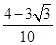
解析试题分析:(1)由已知及向量数量积的坐标运算可求得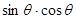 的值,从而应用平方关系就可求得(sinθ+cosθ)2的值,再注意到θ为锐角,知sinθ+cosθ>0,开方即得所求式子的值;(2)由向量平行的坐标条件:
的值,从而应用平方关系就可求得(sinθ+cosθ)2的值,再注意到θ为锐角,知sinθ+cosθ>0,开方即得所求式子的值;(2)由向量平行的坐标条件: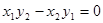 可得
可得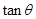 的值,法一:由
的值,法一:由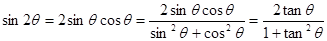 (万能公式)得到
(万能公式)得到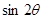 的值,同理可得
的值,同理可得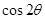 的值;再利用正弦和角公式将sin(2θ+
的值;再利用正弦和角公式将sin(2θ+ )展开即可求得其值;法二:也可由
)展开即可求得其值;法二:也可由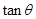 的值,应用三角函数的定义求得
的值,应用三角函数的定义求得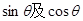 的值,进而用倍角公式可求得
的值,进而用倍角公式可求得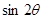 和
和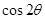 的值,下同法一.
的值,下同法一.
试题解析:(1) 因为a·b=2+sinθcosθ=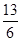 ,所以sinθcosθ=
,所以sinθcosθ=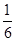 .
.
所以 (sinθ+cosθ)2=1+2 sinθcosθ=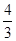 .
.
又因为θ为锐角,所以sinθ+cosθ=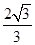 .
.
(2) 解法一 因为a∥b,所以tanθ=2.
所以 sin2θ=2 sinθcosθ=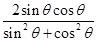 =
=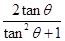 =
=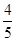 ,
,
cos2θ=cos2θ-sin2θ=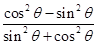 =
=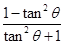 =-
=-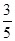 .
.
所以sin(2θ+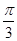 )=
)=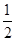 sin2θ+
sin2θ+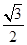 cos2θ=
cos2θ=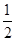 ×
×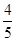 +
+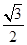 ×(-
×(-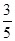 )=
)=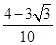 .
.
解法二 因为a∥b,所以tanθ=2.所以 sinθ=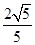 ,cosθ=
,cosθ=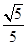 .
.
因此 sin2θ=2 sinθcosθ=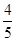 , cos2θ=cos2θ-sin2θ=-
, cos2θ=cos2θ-sin2θ=-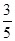 .
.
所以sin(2θ+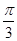 )=
)=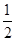 sin2θ+
sin2θ+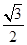 cos2θ=
cos2θ=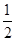 ×
×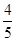 +
+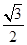 ×(-
×(-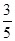 )=
)=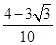 .
.
考点:1.向量的数量积;2.向量平行;3.三角公式.

练习册系列答案
相关题目
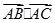 等于 。
等于 。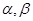 的始边为
的始边为 轴的非负半轴,点
轴的非负半轴,点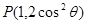 在角
在角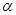 的终边上,点Q
的终边上,点Q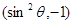 在角
在角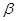 的终边上,且
的终边上,且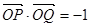 .
.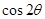 ;
; 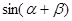 的值.
的值.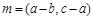 ,
,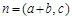 ,且
,且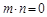
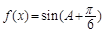 的值域.
的值域. 中,
中, ,
, ,设
,设 .
. 时,求
时,求 的值;
的值; ,求
,求 的值.
的值.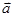 =(cos
=(cos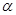 ,sin
,sin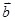 =(cos
=(cos ,sin
,sin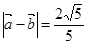 。
。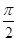 ,-
,-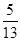 ,求sin
,求sin
 求(1)
求(1) ;(2)
;(2) .
.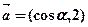 ,
,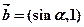 且
且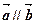 ,则
,则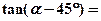
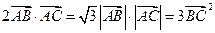 ,求角A、B、C的大小.
,求角A、B、C的大小.