题目内容
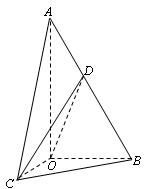 如图,在
如图,在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以直线
以直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 是直二面角.动点
是直二面角.动点![]() 的斜边
的斜边![]() 上.
上.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 为
为![]() 的中点时,求异面直线
的中点时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(Ⅲ)求![]() 与平面
与平面![]() 所成角的最大值
所成角的最大值
解法一:
(Ⅰ)由题意,![]() ,
,![]() ,
,
![]() 是二面角
是二面角![]() 是直二面角,
是直二面角,
又![]() 二面角
二面角![]() 是直二面角,
是直二面角,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.
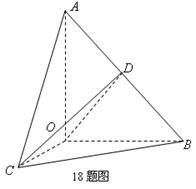
(Ⅱ)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() (如图),则
(如图),则![]() ,
,

![]() 是异面直线
是异面直线![]() 与
与![]() 所成的角.
所成的角.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
又![]() .
.
![]() 在
在![]() 中,
中,![]() .
.
![]() 异面直线
异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
(Ⅲ)由(Ⅰ)知,![]() 平面
平面![]() ,
,
![]() 是
是![]() 与平面
与平面![]() 所成的角,且
所成的角,且![]() .
.
当![]() 最小时,
最小时,![]() 最大,
最大,
这时,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() ,
,
![]() 与平面
与平面![]() 所成角的最大值为
所成角的最大值为![]() .
.
解法二:
(I)同解法一.
(II)建立空间直角坐标系![]() ,如图,则
,如图,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴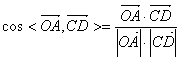
![]() .
.
![]() 异面直线
异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
(Ⅲ)同解法一

练习册系列答案
相关题目

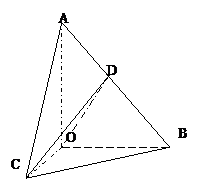 如图,在
如图,在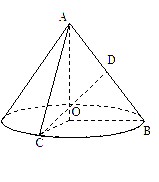
 如图,在
如图,在 中,
中,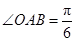 ,斜边
,斜边 .
.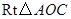 可以通过
可以通过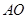 为轴旋转得到,且二面角
为轴旋转得到,且二面角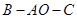 是直二面角.动点
是直二面角.动点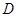 的斜边
的斜边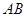 上.
上.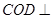 平面
平面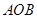 ;
;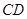 所成角的大小;
所成角的大小;