题目内容
如图,在![]() 中,
中,![]() ,斜边
,斜边![]() ,
,![]() 是
是![]() 的中点.现将
的中点.现将![]() 以直角边
以直角边![]() 为轴旋转一周得到一个圆锥体,点
为轴旋转一周得到一个圆锥体,点![]() 为圆锥体底面圆周上的一点,且
为圆锥体底面圆周上的一点,且![]() .
.
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
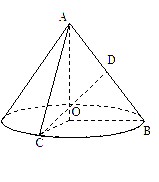
(2)若某动点在圆锥体侧面上运动,试求该动点从点![]() 出发运动到点
出发运动到点![]() 所经过的最短距离.
所经过的最短距离.
(1)![]() (2)
(2)![]()
解析:
(1)解法一:设![]() 中点为
中点为![]() ,联结
,联结![]() 、
、![]() ,
,
则设异面直线![]() 与
与![]() 所成角即为
所成角即为![]() .
. 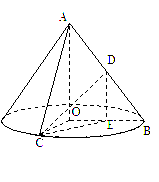
由![]() ,所以
,所以![]() 底面
底面![]() ,于是
,于是![]() .
.
又![]() ,
,![]() ,
,
因此,![]() . 即异面直线
. 即异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
解法二:以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,
则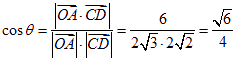 .
.
![]() 异面直线
异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
(2)由条件,底面圆周长为![]() ,母线长
,母线长![]() .
.
故该圆锥体侧面展开图的扇形圆心角大小为![]() ,
,
即展开图恰好为一个半圆(如图). 
由条件![]() ,故展开图中,
,故展开图中, ![]() ,此时
,此时![]() 的长即为所求.
的长即为所求.
由余弦定理,![]() ,
,
故从点C出发在圆锥体表面运动到点D的最短距离为![]() .
.

练习册系列答案
相关题目

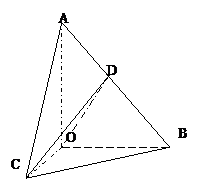 如图,在
如图,在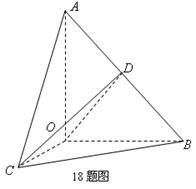 如图,在
如图,在 中,
中,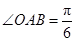 ,斜边
,斜边 .
.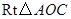 可以通过
可以通过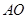 为轴旋转得到,且二面角
为轴旋转得到,且二面角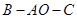 是直二面角.动点
是直二面角.动点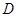 的斜边
的斜边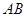 上.
上.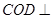 平面
平面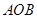 ;
;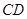 所成角的大小;
所成角的大小;