题目内容
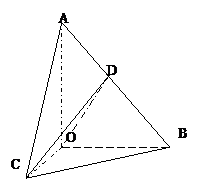 如图,在
如图,在![]() 中,
中,![]() ,斜边
,斜边![]() ,
,![]() 可通过
可通过![]() 以直线AO为轴旋转得到,且二面角
以直线AO为轴旋转得到,且二面角![]() 是直二面角,动点D在斜边AB上,(1)求证:平面
是直二面角,动点D在斜边AB上,(1)求证:平面![]() 平面
平面![]() ;(2)当D为AB的中点时,求异面直线AO与CD所成角的正切值;(3)求CD与平面
;(2)当D为AB的中点时,求异面直线AO与CD所成角的正切值;(3)求CD与平面![]() 所成最大值角的正切值.
所成最大值角的正切值.
(2)![]() (3)
(3)![]()
解析:
证明:(1)由题意得![]() 是二面角
是二面角![]() 的平面角,因二面角
的平面角,因二面角![]() 是直二面角,因此
是直二面角,因此![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,因此平面
,因此平面![]() 平面
平面![]() ;
;
(2)作DE![]() ,垂直为E,连接CE,如图所示,因DE//AO,
,垂直为E,连接CE,如图所示,因DE//AO,![]() 是异面直线AO与CD所成的角,在直角三角形COE中,CO=BO=2,
是异面直线AO与CD所成的角,在直角三角形COE中,CO=BO=2,![]() ,又
,又![]() ,所以在直角三角形
,所以在直角三角形![]() 中有,
中有,![]() 所以异面直线AO与CD所成角的正切值为
所以异面直线AO与CD所成角的正切值为![]() ;
;
(3)由(1)知![]() 平面
平面![]() ,因此
,因此![]() 是CD与平面
是CD与平面![]() 所成的角,且
所成的角,且![]() ,当OD最小时,
,当OD最小时,![]() 最大,这时对于
最大,这时对于![]() ,垂足为D,OD=
,垂足为D,OD=![]() ,因此CD与平面
,因此CD与平面![]() 所成最大值角的正切值为
所成最大值角的正切值为![]() .
.

练习册系列答案
相关题目

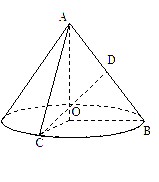
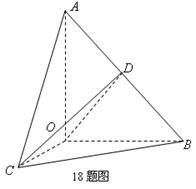 如图,在
如图,在 中,
中,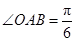 ,斜边
,斜边 .
.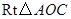 可以通过
可以通过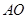 为轴旋转得到,且二面角
为轴旋转得到,且二面角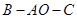 是直二面角.动点
是直二面角.动点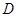 的斜边
的斜边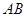 上.
上.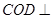 平面
平面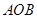 ;
;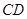 所成角的大小;
所成角的大小;