题目内容
已知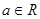 ,函数
,函数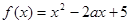 .
.
⑴若不等式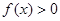 对任意
对任意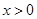 恒成立,求实数
恒成立,求实数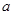 的最值范围;
的最值范围;
⑵若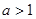 ,且函数
,且函数 的定义域和值域均为
的定义域和值域均为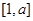 ,求实数
,求实数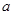 的值.
的值.
(1)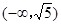 ;(2)
;(2)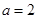 .
.
解析试题分析:(1)根据题意,若不等式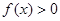 对任意
对任意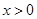 恒成立,参编分离后即可得:
恒成立,参编分离后即可得: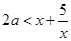 ,从而问题等价于求使
,从而问题等价于求使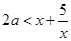 对于任意
对于任意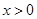 恒成立的
恒成立的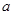 的范围,而
的范围,而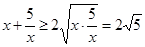 ,当且仅当
,当且仅当 时,“=”成立,故实数
时,“=”成立,故实数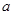 的取值范围是
的取值范围是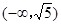 ;(2)由题意可得
;(2)由题意可得 为二次函数,其对称轴为
为二次函数,其对称轴为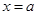 ,因此当
,因此当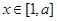 时,可得其值域应为
时,可得其值域应为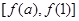 ,从而结合条件
,从而结合条件 的定义域和值域都是
的定义域和值域都是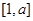 可得关于
可得关于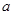 的方程组
的方程组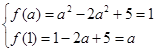 ,即可解得
,即可解得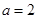 .
.
试题解析:(1)∵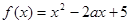 ,∴
,∴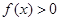 可变形为:
可变形为: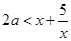 ,而
,而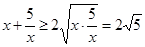 ,当且仅当
,当且仅当 时,“=”成立,∴要使不等式
时,“=”成立,∴要使不等式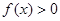 对任意
对任意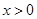 恒成立,只需
恒成立,只需 ,即实数
,即实数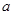 的取值范围是
的取值范围是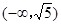 ;
;
(2)∵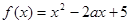 ,∴其图像对称轴为
,∴其图像对称轴为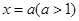 ,根据二次函数的图像,可知
,根据二次函数的图像,可知 在
在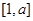 上单调递减,∴当
上单调递减,∴当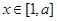 时,其值域为
时,其值域为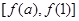 ,又由
,又由 的值域是
的值域是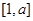 ,
,
∴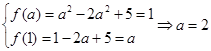 .
.
考点:1.恒成立问题的处理方法;2.二次函数的值域.

练习册系列答案
相关题目
如图所示,n台机器人M1,M2,……,Mn位于一条直线上,检测台M在线段M1 Mn上,n台机器人需把各自生产的零件送交M处进行检测,送检程序设定:当Mi把零件送达M处时,Mi+1即刻自动出发送检(i=1,2,……,n-1)已知Mi的送检速度为V(V>0), 且 记
记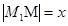 ,n台机器人送检时间总和为f(x).
,n台机器人送检时间总和为f(x).
 |
(1)求f(x)的表达式;
(2)当n=3时,求x的值使得f(x)取得最小值;
(3)求f(x)取得最小值时,x的取值范围.
有一种密英文的明文(真实文)按字母分解,其中英文的a,b,c, ,z的26个字母(不分大小写),依次对应1,2,3, ,26这26个自然数,见如下表格:
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
给出如下变换公式:
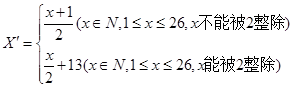
将明文转换成密文,如
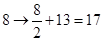 ,即
,即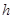 变成
变成 ;如
;如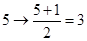 ,即
,即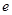 变成
变成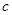 .
.(1)按上述规定,将明文
 译成的密文是什么?
译成的密文是什么?(2)按上述规定,若将某明文译成的密文是
 ,那么原来的明文是什么?
,那么原来的明文是什么? 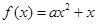
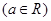
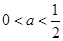 时,
时,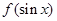
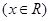 的最大值为
的最大值为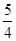 ,求
,求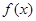 的最小值;
的最小值; ,总有
,总有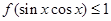 ,试求
,试求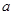 的取值范围.
的取值范围.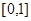 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件: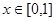 ,总有
,总有 ;
;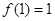 ;
; 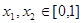 ,且
,且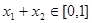 时,
时,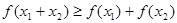 成立.
成立.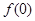 的值;
的值;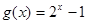 在区间
在区间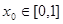 ,使得
,使得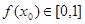 ,且
,且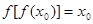 ,求证:
,求证: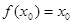 .
.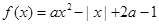 (
( 为实常数).
为实常数).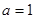 ,求函数
,求函数 的单调区间;
的单调区间;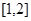 上的最小值为
上的最小值为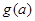 ,求
,求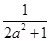 对称,求b的最小值.
对称,求b的最小值.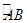 上选择一点C建造垃圾处理厂,其对市区的影响度与所选地
上选择一点C建造垃圾处理厂,其对市区的影响度与所选地 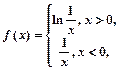 则
则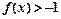 的解集为________.
的解集为________.