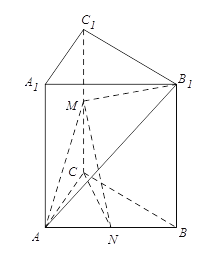
题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,
的中点,![]() 为棱
为棱![]() 上的一点,且
上的一点,且![]() //平面
//平面![]() .
.
(1)求![]() 的值;
的值;
(2)求证:![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() ;(2)详见解析;(3)二面角
;(2)详见解析;(3)二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】
试题分析:(1)求![]() 的值,关键是找
的值,关键是找![]() 在
在![]() 的位置,注意到
的位置,注意到![]() 平面
平面![]() ,有线面平行的性质,可得
,有线面平行的性质,可得![]() ,由已知
,由已知![]() 为
为![]() 中点,由平面几何知识可得
中点,由平面几何知识可得![]() 为
为![]() 中点,从而可得
中点,从而可得![]() 的值;(2)求证:
的值;(2)求证:![]() ,有图观察,用传统方法比较麻烦,而本题由于
,有图观察,用传统方法比较麻烦,而本题由于![]() 底面
底面![]() ,所以
,所以![]() ,
,![]() ,又
,又![]() ,这样建立空间坐标比较简单,故以
,这样建立空间坐标比较简单,故以![]() 为原点,以
为原点,以![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,取
,取![]() ,可写出个点坐标,从而得向量
,可写出个点坐标,从而得向量![]() 的坐标,证
的坐标,证![]() 即可;(3)求二面角
即可;(3)求二面角![]() 的余弦值,由题意可得向量
的余弦值,由题意可得向量![]() 是平面
是平面![]() 的一个法向量,只需求出平面
的一个法向量,只需求出平面![]() 的一个法向量,可设平面
的一个法向量,可设平面![]() 的法向量
的法向量![]() ,利用
,利用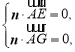 ,即可求出平面
,即可求出平面![]() 的一个法向量,利用向量的夹角公式即可求出二面角
的一个法向量,利用向量的夹角公式即可求出二面角![]() 的余弦值.
的余弦值.
(1)因为![]() 平面
平面![]()
又![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() . 3分
. 3分
因为![]() 为
为![]() 中点,且侧面
中点,且侧面![]() 为平行四边形
为平行四边形
所以![]() 为
为![]() 中点,所以
中点,所以![]() . 4分
. 4分
(2)因为![]() 底面
底面![]() ,
,
所以![]() ,
,![]() , 5分
, 5分
又![]() ,
,
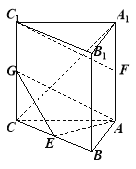
如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,设
,设![]() ,则由
,则由![]() 可得
可得![]() 6分
6分
因为![]() 分别是
分别是![]() 的中点,
的中点,
所以![]() . 7分
. 7分
![]() . 8分
. 8分
所以![]() ,
,
所以![]() . 9分
. 9分

(3)设平面![]() 的法向量
的法向量![]() ,则
,则
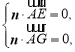 即
即![]() 10分
10分
令![]() ,则
,则![]() ,所以
,所以![]() . 11分
. 11分
由已知可得平面![]() 的法向量
的法向量![]() 11分
11分
所以![]() 13分
13分
由题意知二面角![]() 为钝角,
为钝角,
所以二面角![]() 的余弦值为
的余弦值为![]() . 14分
. 14分

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目