题目内容
已知函数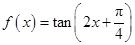 .
.
(Ⅰ)求函数的定义域与最小正周期;
(Ⅱ)设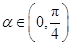 ,若
,若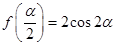 ,求
,求 的大小.
的大小.
(I)函数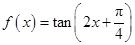 的定义域为
的定义域为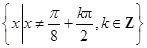 ,最小正周期为
,最小正周期为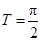 ;
;
(Ⅱ)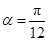 .
.
解析试题分析:(I)利用正切函数的定义域,列出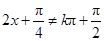 ,
,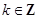 ,由此可以求得函数
,由此可以求得函数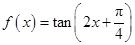 的定义域;利用公式
的定义域;利用公式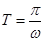 ,可以求得函数
,可以求得函数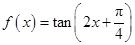 的最小正周期;
的最小正周期;
(Ⅱ)由已知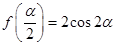 ,首先列式:
,首先列式: ,利用两角和的正弦、余弦、正切公式,同角三角函数的基本关系以及二倍角的正弦、余弦公式化简,解方程并注意角
,利用两角和的正弦、余弦、正切公式,同角三角函数的基本关系以及二倍角的正弦、余弦公式化简,解方程并注意角 的范围(
的范围(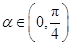 ),即可求得角
),即可求得角 的值.
的值.
试题解析:
(Ⅰ)函数的定义域满足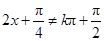 ,
,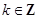 ,解得
,解得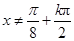 ,
,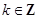 .所以函数的定义域为
.所以函数的定义域为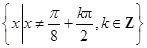 .最小正周期为
.最小正周期为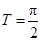 .
.
(Ⅱ) 解法1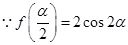 :,
:, ,
,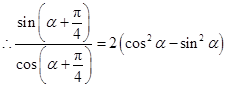 ,于是
,于是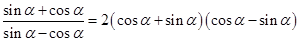 ,因为
,因为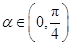 ,所以
,所以 ,所以
,所以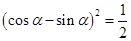 ,因而
,因而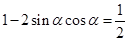 ,
,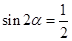 ,因为
,因为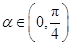 ,所以
,所以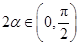 ,所以
,所以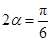 ,
,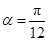 .
.
解法2:因为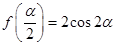 ,所以
,所以 ,
,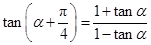 ,
,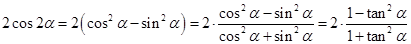 ,
,
所以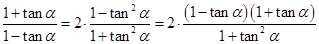 ,
,
因为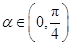 ,所以
,所以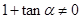 ,于是
,于是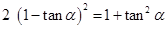 ,
,
整理得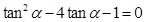 ,所以
,所以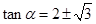 ,
,
因为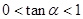 ,所以
,所以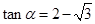 ,因此
,因此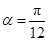 .
.
解法3: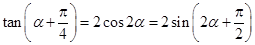 ,
,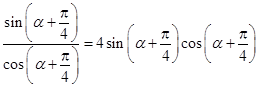 ,
,
因为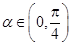 ,所以
,所以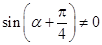 ,得
,得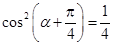 .
.
故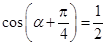 ,于是
,于是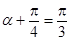 .所以
.所以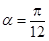 .
.
考点:1.两角和的正弦、余弦、正切公式;2.同角三角函数的基本关系;3.二倍角的正弦、余弦公式;4.正切函数的性质.

练习册系列答案
相关题目
 (
( )的最小正周期为
)的最小正周期为 .
. 的单调增区间;
的单调增区间; 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数 的图象.求
的图象.求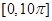 上零点的个数.
上零点的个数. =
= -sin(2x-
-sin(2x- ).
).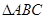 的内角
的内角 的对边分别为
的对边分别为 ,
, ,f(
,f( )=
)= ,若
,若 ,求
,求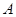 、
、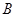 、
、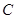 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点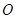 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为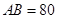
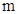 ,
,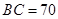
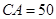
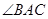 的大小;
的大小;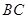 的距
的距 中,内角
中,内角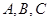 所对边长分别为
所对边长分别为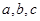 ,
,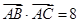 ,
,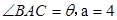 .
.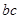 的最大值; (2)求函数
的最大值; (2)求函数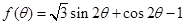 的值域.
的值域.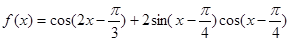 (
(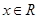 ).
). 的最小正周期;
的最小正周期;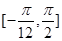 上的值域.
上的值域.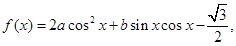 x∈R且
x∈R且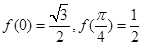 ,
, 的最小正周期;
的最小正周期; 中,
中,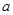 、
、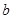 、
、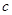 是三个内角
是三个内角 、
、 、
、 的对边,关于
的对边,关于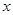 的不等式
的不等式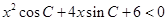
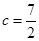 ,
,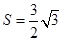 ,求当角
,求当角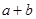 的值.
的值.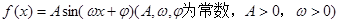 的部分图像如图所示,
的部分图像如图所示,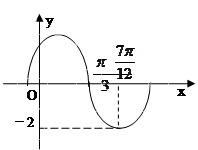
 的解析式;
的解析式;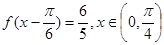 ,求
,求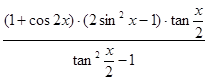 的值。
的值。