题目内容
抛物线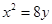 的准线与
的准线与 轴交于点
轴交于点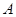 ,点
,点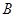 在抛物线对称轴上,过
在抛物线对称轴上,过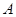 可作直线交抛物线于点
可作直线交抛物线于点 、
、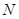 ,使得
,使得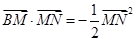 ,则
,则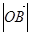 的取值范围是 .
的取值范围是 .
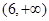
解析试题分析:由题意可得A(0,-2),直线MN的斜率k存在且k≠0,
设直线MN的方程为y=kx-2,联立方程组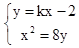 ,得x2-8kx+16=0,
,得x2-8kx+16=0,
设M (x1,x2),N(x2,y2),MN 的中点E(x0,y0),
则△=64k2-64>0,即k2>1,
x1+x2=8k,y1+y2=k(x1+x2)-4=-4+8k2,
∴x0=4k,y0=-2+4k2即E(4k,-2+4k2).
∵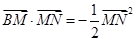 ,
,
∴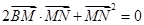 ,即
,即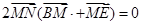 ,而
,而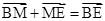 ,
,
∴BE⊥MN即点B在MN的垂直平分线上,
∵MN的斜率为k,E(4k,-2+4k2).
∴MN的垂直平分线BE的方程为:y-4k2+2=-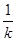 (x-4k),与y轴的交点即是B,
(x-4k),与y轴的交点即是B,
令x=0可得,y=2+4k2,
则|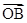 |=2+4k2>6.
|=2+4k2>6.
故答案为(6,+∞).
考点:本题主要考查平面向量的线性运算、数量积,直线与抛物线的位置关系。
点评:中档题,本题主要考查了平面向量的线性运算、数量积,直线与抛物线的位置关系。在研究过程中运用方程的根与系数关系,使问题得到简化。

练习册系列答案
相关题目
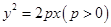 的准线经过椭圆
的准线经过椭圆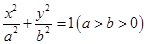 的左焦点,且经过抛物线与椭圆两个交点的弦过抛物线的焦点,则椭圆的离心率为_____________
的左焦点,且经过抛物线与椭圆两个交点的弦过抛物线的焦点,则椭圆的离心率为_____________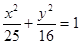 上一点
上一点 到椭圆一个焦点的距离是3,则
到椭圆一个焦点的距离是3,则 的端点
的端点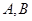 分别在
分别在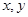 轴上移动,动点
轴上移动,动点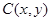 满足
满足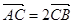 ,则动点
,则动点 的轨迹方程是 .
的轨迹方程是 .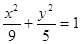 左焦点
左焦点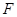 且不垂直于x轴的直线交椭圆于A、B两点,AB的垂直平分线交x轴于点
且不垂直于x轴的直线交椭圆于A、B两点,AB的垂直平分线交x轴于点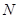 ,则
,则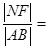 ;
;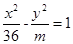 的离心率
的离心率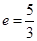 ,则
,则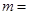 。
。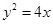 的焦点
的焦点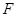 的直线交抛物线于
的直线交抛物线于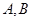 两点,满足
两点,满足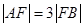 ,则弦
,则弦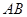 的中点到准线的距离为____.
的中点到准线的距离为____.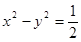 与椭圆有公共的焦点,且它们的离心率互为倒数,则该椭圆的标准方程为___________________。
与椭圆有公共的焦点,且它们的离心率互为倒数,则该椭圆的标准方程为___________________。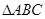 为直角三角形,三边长分别为
为直角三角形,三边长分别为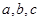 ,其中斜边AB=
,其中斜边AB=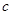 ,若点
,若点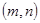 在直线
在直线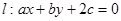 上运动,则
上运动,则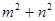 的最小值为
的最小值为