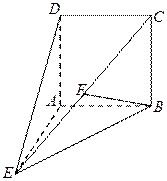题目内容
(本小题满分12分)
如图,在三棱柱ADF—BCE中,侧棱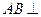 底面
底面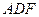 ,底面
,底面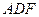 是等腰直角三角形,且
是等腰直角三角形,且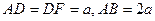 ,M、G分别是AB、DF的中点.
,M、G分别是AB、DF的中点.
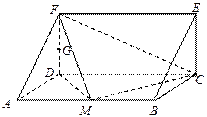
(1)求证GA∥平面FMC;
(2)求直线DM与平面ABEF所成角。
如图,在三棱柱ADF—BCE中,侧棱
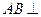 底面
底面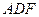 ,底面
,底面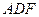 是等腰直角三角形,且
是等腰直角三角形,且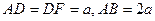 ,M、G分别是AB、DF的中点.
,M、G分别是AB、DF的中点. 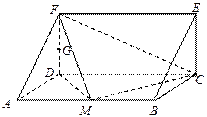
(1)求证GA∥平面FMC;
(2)求直线DM与平面ABEF所成角。
解:
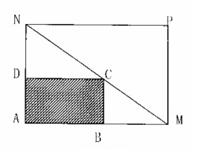
(1)证明:取DC中点S,连接AS、GS、GA
∵G是DF的中点,GS//FC,AS//CM
∴面GSA//面FMC,而GA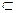 面GSA,
面GSA,
∴GA//平面FMC 6分
(2)在平面ADF上,过D作AF的垂线,
垂足为H ,连DM,则DH⊥平面ABEF,
,连DM,则DH⊥平面ABEF,
∠DMH是DM与平面ABEF所成的角。 8分
在RTDHM中, 。
。
所以DM与平面ABEF所成的角为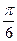 。 12分
。 12分

(1)证明:取DC中点S,连接AS、GS、GA
∵G是DF的中点,GS//FC,AS//CM
∴面GSA//面FMC,而GA
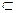 面GSA,
面GSA,∴GA//平面FMC 6分
(2)在平面ADF上,过D作AF的垂线,
垂足为H
 ,连DM,则DH⊥平面ABEF,
,连DM,则DH⊥平面ABEF,∠DMH是DM与平面ABEF所成的角。 8分
在RTDHM中,
 。
。所以DM与平面ABEF所成的角为
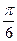 。 12分
。 12分略

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
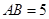 ,AA1=4,.点D是AB的中点.
,AA1=4,.点D是AB的中点.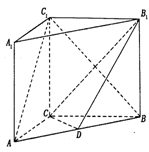
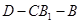 的平面角的正切值.
的平面角的正切值.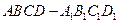 中,
中,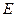 、
、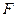 分别为
分别为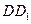 、
、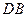 的中点. (1)求证: (1)、
的中点. (1)求证: (1)、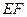 //平面
//平面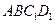 ;
;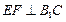 ;
;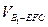 的体积.
的体积.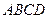 中,
中,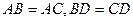 ,平面
,平面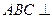 平面
平面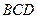 ,
,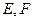 分别为棱
分别为棱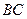 和
和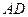 的中点。
的中点。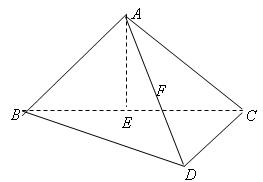
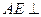 平面
平面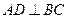 ;
;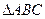 内的点
内的点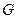 满足
满足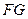 ∥平面
∥平面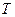 ,试描述点集
,试描述点集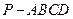 的底面
的底面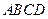 为一直角梯形,其中
为一直角梯形,其中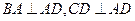 ,
,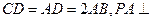 底面
底面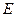 是
是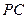 的中点.
的中点.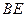 //平面
//平面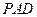 ;
;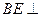 平面
平面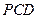 ,
,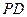 与
与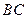 所成角的余弦值;
所成角的余弦值;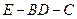 的余弦值.
的余弦值.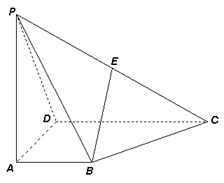
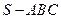 中,
中,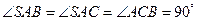 ,且
,且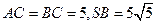 。
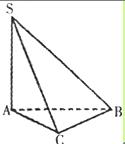
。
 ;
;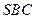 与底面
与底面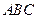 所成二面角的大小;
所成二面角的大小; 面ABCD,
面ABCD,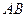 ∥
∥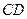 ,AD=CD=1,∠
,AD=CD=1,∠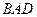 =120°,
=120°,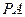 =
=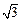 ,∠
,∠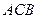 =90°,M是线段PD上的一点(不包括端点).
=90°,M是线段PD上的一点(不包括端点).
 C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是( )
C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是( )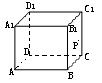
 如图,正方形
如图,正方形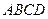 所在平面与
所在平面与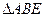 所在平面垂直,
所在平面垂直,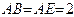 ,
,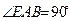 ,
,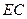 中点为
中点为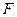 .
.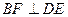
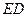 与平面
与平面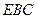 所成角
所成角