题目内容
给出下列四个命题,其中错误的命题有( )个.
(1)将函数y=sin(2x+
)的图象向右平移
个单位,得到函数y=sin2x的图象;
(2)函数y=sin2x+cos2x在x∈[0,
]上的单调递增区间是[0,
];
(3)设A、B、C∈(0,
)且sinA-sinC=sinB,cosA+cosC=cosB,则B-A等于-
;
(4)方程sin2x+2sinx+a=0有解,则a的取值范围是[-3,1].
(5)在同一坐标系中,函数y=sinx与函数y=
的图象有三个交点.
(1)将函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
(2)函数y=sin2x+cos2x在x∈[0,
| π |
| 2 |
| π |
| 8 |
(3)设A、B、C∈(0,
| π |
| 2 |
| π |
| 3 |
(4)方程sin2x+2sinx+a=0有解,则a的取值范围是[-3,1].
(5)在同一坐标系中,函数y=sinx与函数y=
| x |
| 2 |
分析:(1)根据函数的左加右减的原则即可求解平移后的函数解析式
(2)由y=sin2x+cos2x=
sin(2x+
),结合正弦函数的性质可求函数的单调区间
(3)由sinA-sinC=sinB,cosA+cosC=cosB,可得sinC=sinA-sinB,cosC=cosB-cosA,两边同时平方相加可求cos(B-A)=
结合sinA-sinC=sinB>0可得A>B,可求
(4)sin2x+2sinx=(sinx+1)2-1,结合正弦函数与二次函数的性质可求函数的值域,进而可求a的范围
(5)由于x=0时,两函数相交,当0<x≤2时,有一个交点,当-2≤x<0时,,有一个交点,当x>2或x<-2时两函数的图象没有交点,可判断
(2)由y=sin2x+cos2x=
| 2 |
| π |
| 4 |
(3)由sinA-sinC=sinB,cosA+cosC=cosB,可得sinC=sinA-sinB,cosC=cosB-cosA,两边同时平方相加可求cos(B-A)=
| 1 |
| 2 |
结合sinA-sinC=sinB>0可得A>B,可求
(4)sin2x+2sinx=(sinx+1)2-1,结合正弦函数与二次函数的性质可求函数的值域,进而可求a的范围
(5)由于x=0时,两函数相交,当0<x≤2时,有一个交点,当-2≤x<0时,,有一个交点,当x>2或x<-2时两函数的图象没有交点,可判断
解答:解:(1)将函数y=sin(2x+
)的图象向右平移
个单位,得到函数y=sin(2x-
π)的图象;故(1)错误
(2)∵y=sin2x+cos2x=
sin(2x+
)
令-
π≤2x+
≤
π可得,-
≤x≤
∴函数y=sin2x+cos2x在x∈[0,
]上的单调递增区间是[0,
];(2)正确
(3)由sinA-sinC=sinB,cosA+cosC=cosB,可得sinC=sinA-sinB,cosC=cosB-cosA,
两边同时平方相加可得1=2-2(cosAcosB+sinAsinB)=2-2cos(A-B)
∴cos(B-A)=
∵sinA-sinC=sinB>0
∴sinA>sinB
∴A>B
∴B-A=
(3)正确
(4)∵sin2x+2sinx=(sinx+1)2-1∈[-1,3]
∵sin2x+2sinx+a=0有解,
-1≤-a≤3
∴-3≤a≤1
则a的取值范围是[-3,1],(4)正确
(5)由于x=0时,两函数相交,
当0<x≤2时,函数y=sinx与函数y=
的图象有一个交点,
当-2≤x<0时,,函数y=sinx与函数y=
的图象有一个交点,
当x>2或x<-2时,|
|>1,而sinx≤1,两函数的图象没有交点,即有3个交点,(5)正确
即错误的命题有1个
故选A
| π |
| 3 |
| π |
| 3 |
| 1 |
| 3 |
(2)∵y=sin2x+cos2x=
| 2 |
| π |
| 4 |
令-
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
∴函数y=sin2x+cos2x在x∈[0,
| π |
| 2 |
| π |
| 8 |
(3)由sinA-sinC=sinB,cosA+cosC=cosB,可得sinC=sinA-sinB,cosC=cosB-cosA,
两边同时平方相加可得1=2-2(cosAcosB+sinAsinB)=2-2cos(A-B)
∴cos(B-A)=
| 1 |
| 2 |
∵sinA-sinC=sinB>0
∴sinA>sinB
∴A>B
∴B-A=
| π |
| 3 |
(4)∵sin2x+2sinx=(sinx+1)2-1∈[-1,3]
∵sin2x+2sinx+a=0有解,
-1≤-a≤3
∴-3≤a≤1
则a的取值范围是[-3,1],(4)正确
(5)由于x=0时,两函数相交,
当0<x≤2时,函数y=sinx与函数y=
| x |
| 2 |
当-2≤x<0时,,函数y=sinx与函数y=
| x |
| 2 |
当x>2或x<-2时,|
| x |
| 2 |
即错误的命题有1个
故选A
点评:本题主要考查了命题的真假关系的判断,解题的关键是熟练掌握基本知识,此类问题的具有一定的综合性

练习册系列答案
相关题目


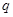 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 ”的既不充分也不必要条件;
”的既不充分也不必要条件; 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
; 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
; 与
与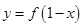 图像关于
图像关于 对称.
对称.