题目内容
若数列 的前
的前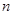 项和为
项和为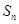 ,对任意正整数
,对任意正整数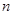 都有
都有 ,记
,记 .
.
(1)求 ,
, 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)若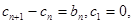 求证:对任意
求证:对任意 .
.
(1)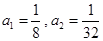 ;(2)
;(2)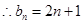 ;(3)见试题解析.
;(3)见试题解析.
解析试题分析:(1)分别令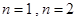 可求得
可求得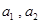 的值;(2)利用
的值;(2)利用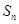 与
与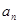 的关系式,先求
的关系式,先求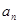 ,再利用已知条件
,再利用已知条件 求得数列
求得数列 的通项公式;(3)先利用累加法求得
的通项公式;(3)先利用累加法求得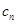 ,再利用裂项相消法求和
,再利用裂项相消法求和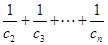 ,进而可证明不等式.
,进而可证明不等式.
试题解析:(1)由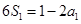 ,得
,得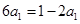 ,解得
,解得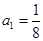 . 1分
. 1分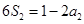 ,得
,得 ,解得
,解得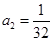 . 3分
. 3分
(2)由 ①,
①,
当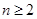 时,有
时,有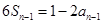 ②, 4分
②, 4分
①-②得: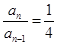 , 5分
, 5分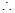 数列
数列 是首项
是首项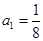 ,公比
,公比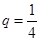 的等比数列 6分
的等比数列 6分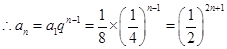 , 7分
, 7分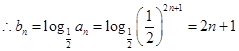 . 8分
. 8分
(3)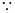
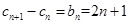 ,
,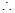
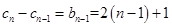 , (1)
, (1)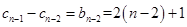 , (2)
, (2)
,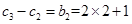 ,
, , (
, (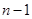 ) 9分
) 9分
(1)+(2)+ +(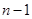 )得
)得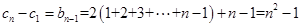 , 10分
, 10分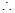
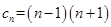 , 11分
, 11分 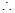
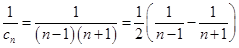 , 12分
, 12分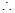
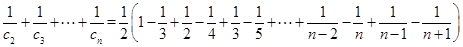
 , 13分
, 13分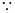
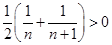 ,
, 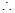
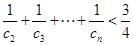 对任意
对任意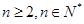 均成立. 14分
均成立. 14分
考点:1、数列通项公式的求法;2、数列前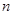 项和的求法;3、数列不等式的证明.
项和的求法;3、数列不等式的证明.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
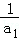 +
+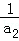 +…+
+…+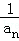 <
<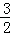 .
. 的首项
的首项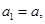 其中
其中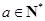 ,
,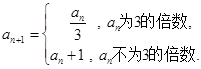 令集合
令集合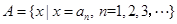 .
.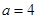 ,写出集合
,写出集合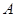 中的所有的元素;
中的所有的元素;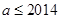 ,且数列
,且数列 的所有可能取值构成的集合;
的所有可能取值构成的集合;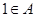 .
.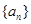 的前
的前 项和为
项和为 ,
,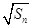 是
是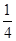 与
与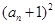 的等比中项.
的等比中项.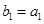 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前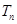 .
.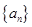 满足:
满足: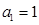 ,
,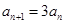 ,
,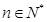 .
. 项和
项和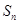 ;
;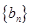 是等差数列,
是等差数列,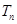 为前
为前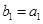 ,
,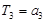 .求
.求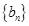 的通项公式,并证明:
的通项公式,并证明: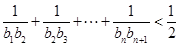 .
.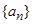 中,
中,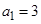 ,前
,前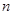 和
和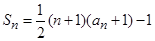
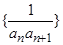 的前
的前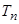 ,是否存在实数
,是否存在实数 ,使得
,使得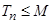 对一切正整数
对一切正整数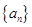 中,
中,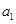 、
、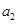 、
、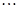 、
、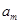 构成首项为2,公差为-2的等差数列,
构成首项为2,公差为-2的等差数列, 、
、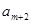 、
、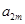 ,构成首项为
,构成首项为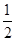 ,公比为
,公比为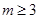 ,
,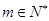 .
.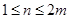 ,
,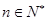 ,都有
,都有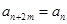 成立.
成立.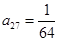 时,求
时,求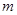 的值;
的值;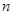 项和为
项和为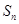 .判断是否存在
.判断是否存在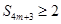 成立?若存在,求出
成立?若存在,求出 满足
满足 .
. ,
, ,
, ,
,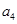 ,由此猜想通项公式
,由此猜想通项公式 ,并用数学归纳法证明此猜想;
,并用数学归纳法证明此猜想; 满足
满足 ,求证:
,求证: .
.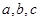 ,求证:
,求证: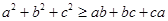 ;
;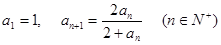 ,写出
,写出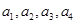 并猜想这个数列的通项公式达式.
并猜想这个数列的通项公式达式.