题目内容
(14分)设各项均为正数的数列 的前n项和为
的前n项和为 ,已知
,已知 ,数
,数
列 是公差为
是公差为 的等差数列。
的等差数列。
(1)求数列 的通项公式(用
的通项公式(用 表示);
表示);
(2)设 为实数,对满足
为实数,对满足 的任意正整数
的任意正整数 ,不等式
,不等式 都成立。求证:
都成立。求证: 的最大值为
的最大值为 。
。
【答案】
解:(1)由题意知: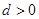 ,
, 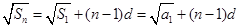
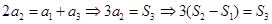 ,
,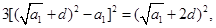
化简,得: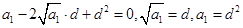
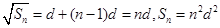 ,
,
当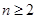 时,
时,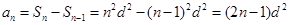 ,适合
,适合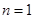 情形。
情形。
故所求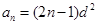
(2)(方法一)
 ,
, 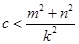 恒成立。
恒成立。
又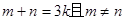 ,
,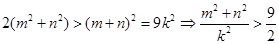 ,
,
故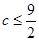 ,即
,即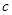 的最大值为
的最大值为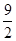 。
。
(方法二)由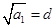 及
及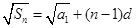 ,得
,得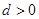 ,
,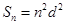 。
。
于是,对满足题设的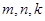 ,
,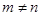 ,有
,有
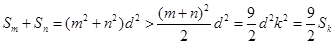 。
。
所以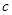 的最大值
的最大值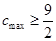 。
。
另一方面,任取实数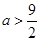 。设
。设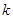 为偶数,令
为偶数,令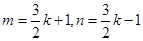 ,则
,则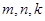 符合条件,
符合条件,
且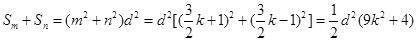 。
。
于是,只要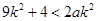 ,即当
,即当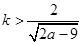 时,
时,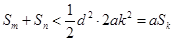 。
。
所以满足条件的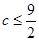 ,从而
,从而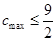 。因此
。因此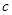 的最大值为
的最大值为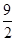 。
。
【解析】略

练习册系列答案
相关题目