题目内容
【题目】函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)若![]() 为定值,求
为定值,求![]() 的最大值;
的最大值;
(2)求证:对任意![]() ,有
,有![]()
![]() ;
;
(3)若![]() ,
,![]() ,求证:对任意
,求证:对任意![]() ,直线
,直线![]() 与曲线
与曲线![]() 有唯一公共点.
有唯一公共点.
【答案】(1)![]() (2)见证明;(3)见证明;
(2)见证明;(3)见证明;
【解析】
(1)n看作常数,函数求导后令导数等于零,可得![]() ,可知函数在
,可知函数在![]() 处有极大值,可得函数最大值(2)取
处有极大值,可得函数最大值(2)取![]() 得
得![]() ,利用放缩法得
,利用放缩法得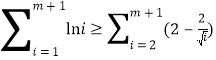
![]() ,再根据裂项相消法求和即可(3)要证明当
,再根据裂项相消法求和即可(3)要证明当![]() ,
,![]() 时,关于
时,关于![]() 的方程
的方程![]() 有唯一解,令
有唯一解,令![]() ,即证明
,即证明![]() 有唯一零点,再利用导数得函数单调性,极值确定函数大致图象,证明只有唯一零点即可.
有唯一零点,再利用导数得函数单调性,极值确定函数大致图象,证明只有唯一零点即可.
(1)![]() 为定值,故
为定值,故![]() ,令
,令![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以函数在
,所以函数在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以当
上单调递减,所以当![]() 时,函数有极大值
时,函数有极大值![]() ,也是最大值,所以
,也是最大值,所以![]() .
.
(2)由前一问可知![]() ,取
,取![]() 得
得![]() ,于是
,于是
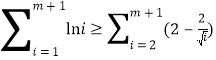
![]()
![]()
![]()
![]() .
.
(3)要证明当![]() ,
,![]() 时,关于
时,关于![]() 的方程
的方程![]() 有唯一解,令
有唯一解,令![]() ,即证明
,即证明![]() 有唯一零点,先证明
有唯一零点,先证明![]() 存在零点,再利用导数得函数单调性,极值确定函数只有唯一零点.
存在零点,再利用导数得函数单调性,极值确定函数只有唯一零点.
我们先证三个引理
【引理1】
![]() (由第1问取
(由第1问取![]() 即可)
即可)
【引理2】
![]() (由【引理1】变形得到)
(由【引理1】变形得到)
【引理3】
![]() (可直接证明也可由【引理2推出】
(可直接证明也可由【引理2推出】
证明:![]() .
.
下面我们先证明函数![]() 存在零点,先由【引理2】得到:
存在零点,先由【引理2】得到:
![]() .
.
令![]() ,可知
,可知![]() .再由【引理3】得到
.再由【引理3】得到![]() ,于是
,于是
![]()
![]() .
.
令![]() ,且
,且![]() ,可知
,可知![]() .由连续性可知该函数一定存在零点.
.由连续性可知该函数一定存在零点.
下面我们开始证明函数![]() 最多只能有一个零点.我们有
最多只能有一个零点.我们有
![]() .
.
令![]() ,则
,则![]() ,则
,则![]() 在
在![]() 递增,在
递增,在![]() 递减,即
递减,即![]() .
.
当![]() 时,有
时,有![]() 恒成立,
恒成立,![]() 在
在![]() 上递增,所以最多一个零点.
上递增,所以最多一个零点.
当![]() 时,令
时,令![]() ,
,![]() ,即
,即![]() ,于是
,于是
![]()
![]() .
.
再令![]() ,由【引理1】可以得到
,由【引理1】可以得到![]() .
.
因此函数![]() 在
在![]() 递增,
递增,![]() 递减,
递减,![]() 递增,
递增,![]() 时,
时,![]() 有极大值但其极大值
有极大值但其极大值![]() ,所以最多只有一个零点.
,所以最多只有一个零点.
综上,当![]() ,
,![]() 时,函数
时,函数![]() 与
与![]() 的图像有唯一交点.
的图像有唯一交点.

【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
【题目】呼和浩特市地铁一号线于2019年12月29日开始正式运营有关部门通过价格听证会,拟定地铁票价后又进行了一次调查.调查随机抽查了50人,他们的月收入情况与对地铁票价格态度如下表:
月收入(单位:百元) |
|
|
|
|
|
|
认为票价合理的人数 | 1 | 2 | 3 | 5 | 3 | 4 |
认为票价偏高的人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)若以区间的中点值作为月收入在该区间内人的人均月收入求参与调查的人员中“认为票价合理者”的月平均收入与“认为票价偏高者”的月平均收入的差是多少(结果保留2位小数);
(2)由以上统计数据填写下面![]() 列联表分析是否有
列联表分析是否有![]() 的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
月收入不低于5500元人数 | 月收入低于5500元人数 | 合计 | |
认为票价偏高者 | |||
认为票价合理者 | |||
合计 |
附:![]()
| 0.05 | 0.01 |
| 3.841 | 6.635 |

