题目内容
已知抛物线C:y2=2px(p>0)过点A(1,-2).
(1)求抛物线C的方程,并求其准线方程.
(2)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于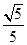 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
(1) 抛物线C的方程为y2=4x 准线方程为x=-1. (2) 存在,其方程为2x+y-1=0
解析解:(1)将(1,-2)代入y2=2px,得(-2)2=2p·1,
所以p=2.
故所求的抛物线C的方程为y2=4x,
其准线方程为x=-1.
(2)假设存在符合题意的直线l,其方程为y=-2x+t.
由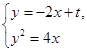 得y2+2y-2t=0.
得y2+2y-2t=0.
因为直线l与抛物线C有公共点,
所以Δ=4+8t≥0,
解得t≥- .
.
另一方面,由直线OA与l的距离d=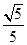 可得
可得 =
= ,
,
解得t=±1.
因为-1∉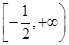 ,1∈
,1∈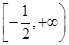 ,
,
所以符合题意的直线l存在,其方程为2x+y-1=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
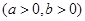 的左焦点
的左焦点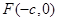
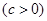 ,作倾斜角为
,作倾斜角为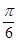 的直线
的直线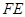 交该双曲线右支于点
交该双曲线右支于点 ,若
,若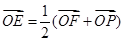 ,且
,且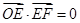 ,则双曲线的离心率为__________.
,则双曲线的离心率为__________. +
+ =1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
=1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|. )2=16相交于M,N两点,且|MN|=
)2=16相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程. 的左顶点
的左顶点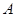 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为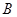 ,与
,与 轴的交点为
轴的交点为 ,已知
,已知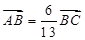 .
.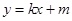 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点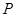 ,且与直线
,且与直线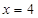 相交于点
相交于点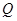 ,若
,若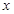 轴上存在一定点
轴上存在一定点 ,使得
,使得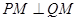 ,求椭圆的方程.
,求椭圆的方程.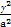 +
+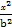 =1(a>b>0)交于A(x1,y1),B(x2,y2)两点,已知m=(ax1,by1),n=(ax2,by2),若m⊥n且椭圆的离心离e=
=1(a>b>0)交于A(x1,y1),B(x2,y2)两点,已知m=(ax1,by1),n=(ax2,by2),若m⊥n且椭圆的离心离e=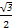 ,又椭圆经过点(
,又椭圆经过点(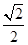 x和y=-
x和y=-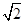 ,设O为坐标原点,动点P满足
,设O为坐标原点,动点P满足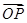 =
=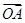 +
+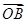 .
.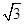 ,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.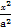 +
+ =1(a>b>0)的右焦点为F(1,0),且点(-1,
=1(a>b>0)的右焦点为F(1,0),且点(-1,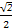 )在椭圆C上.
)在椭圆C上. ,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明:
,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明: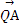 ·
·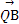 为定值.
为定值.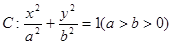 的离心率为
的离心率为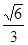 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为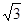 .
.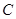 的方程;
的方程;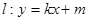 与椭圆
与椭圆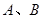 两点,坐标原点
两点,坐标原点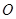 到直线
到直线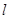 的距离为
的距离为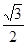 ,求
,求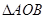 面积的最大值.
面积的最大值.