题目内容
过椭圆 的左顶点
的左顶点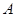 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为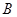 ,与
,与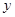 轴的交点为
轴的交点为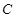 ,已知
,已知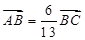 .
.
(1)求椭圆的离心率;
(2)设动直线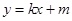 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点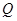 ,若
,若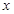 轴上存在一定点
轴上存在一定点 ,使得
,使得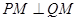 ,求椭圆的方程.
,求椭圆的方程.
(1) ;(2)
;(2) .
.
解析试题分析:(I)根据
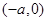 ,设直线方程为
,设直线方程为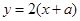 ,
,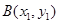
确定 的坐标,由
的坐标,由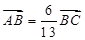 确定得到
确定得到 ,
,
再根据 点在椭圆上,求得
点在椭圆上,求得 进一步即得所求
进一步即得所求 ;
;
(2)由 可设
可设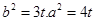 ,
,
得到椭圆的方程为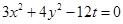 ,
,
由 得
得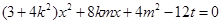
根据动直线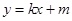 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P
得到 ,整理得
,整理得 .
.
确定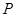 的坐标
的坐标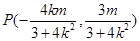 ,
,
又 ,
,

若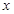 轴上存在一定点
轴上存在一定点 ,使得
,使得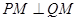 ,那么
,那么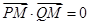
可得 ,由
,由 恒成立,故
恒成立,故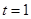 ,得解.
,得解.
试题解析:(1)∵
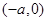 ,设直线方程为
,设直线方程为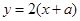 ,
,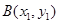
令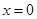 ,则
,则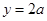 ,∴
,∴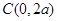 , 2分
, 2分
∴ 3分
3分
∵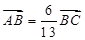 ,∴
,∴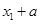 =
= ,
,
整理得 4分
4分
∵ 点在椭圆上,∴
点在椭圆上,∴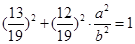 ,∴
,∴ 5分
5分
∴ 即
即 ,∴
,∴ 6分
6分
(2)∵ 可设
可设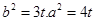 ,
,
∴椭圆的方程为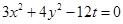 7分
7分
由 得
得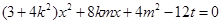 8分
8分
∵动直线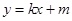 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P
∴ ,即
,即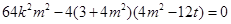
整理得 9分
9分
设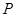
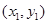 则有
则有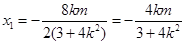 ,
,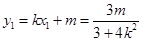
∴

练习册系列答案
相关题目
 的右焦点为
的右焦点为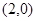 ,实轴长
,实轴长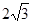 .
.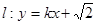 与双曲线恒有两个不同的交点
与双曲线恒有两个不同的交点 ,且
,且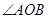 为锐角(其中
为锐角(其中 为原点),求
为原点),求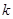 的取值范围.
的取值范围.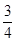 .
. ,直线l:y=kx+
,直线l:y=kx+ 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当 ≤k≤2时,|AB|2+|DE|2的最小值.
≤k≤2时,|AB|2+|DE|2的最小值. ,向量
,向量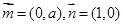 ,经过定点
,经过定点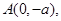 以
以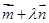 为方向向量的直线与经过定点
为方向向量的直线与经过定点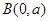 以
以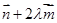 为方向向量的直线相交于
为方向向量的直线相交于 ,其中
,其中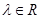 ,
,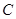 的方程;(2)若
的方程;(2)若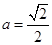 ,过
,过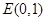 的直线交曲线
的直线交曲线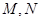 两点,求
两点,求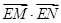 的取值范围。
的取值范围。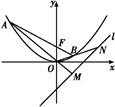
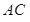 、
、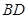 是过抛物线
是过抛物线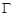 焦点
焦点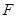 的两条弦,且其焦点
的两条弦,且其焦点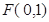 ,
,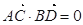 ,点
,点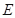 为
为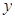 轴上一点,记
轴上一点,记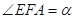 ,其中
,其中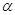 为锐角.
为锐角.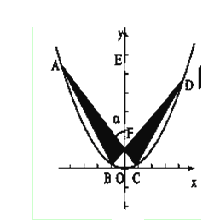
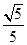 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.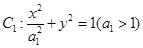 与
与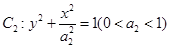 的离心率相等. 直线
的离心率相等. 直线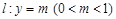 与曲线
与曲线 交于
交于 两点(
两点(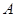 在
在 的左侧),与曲线
的左侧),与曲线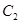 交于
交于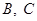 两点(
两点( 在
在 的左侧),
的左侧),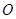 为坐标原点,
为坐标原点,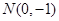 .
.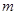 =
=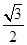 ,
,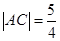 时,求椭圆
时,求椭圆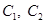 的方程;
的方程;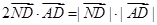 ,且
,且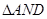 和
和 相似,求
相似,求