题目内容
某校周四下午第五、六两节是选修课时间,现有甲、乙、丙、丁四位教师可开课。已知甲、乙教师各自最多可以开设两节课,丙、丁教师各自最多可以开设一节课.现要求第五、六两节课中每节课恰有两位教师开课(不必考虑教师所开课的班级和内容),则不同的开课方案共有( )种。
| A.20 | B.19 | C.16 | D.15 |
B
试题分析:法一:枚举可得,有下列的开课方案:
(1)第五节:甲,乙,第六节:甲,乙;(2)第五节:甲,乙,第六节:甲,丙(丁);(两种)
(3)第五节:甲,乙,第六节:乙,丙(丁);(两种)(4)第五节:甲,丙(丁),第六节:甲,乙;(两种)(5)第五节:乙,丙(丁),第六节:甲,乙;(两种)(6)第五节:甲,乙,第六节:丙,丁;(7)第五节:甲,丙,第六节:甲,丁;(8)第五节:甲,丙,第六节:乙,丁;(9)第五节:乙,丙,第六节:甲,丁;(10)第五节:乙,丙,第六节:乙,丁;(11)第五节:甲,丁,第六节:甲,丙;(12)第五节:甲,丁,第六节:乙,丙;(13)第五节:乙,丁,第六节:甲,丙;(14)第五节:乙,丁,第六节:乙,丙;(15)第五节:丙,丁,第六节:甲,乙;
综上所述,一共有19种开课方案.
法二:开课方案可以分一下几种情况:(1)丙丁都不上课,有1种方案;(2)丙丁有一个老师上课,有(2+2)×2=8种方案;(3)丙丁老师都上课,有1+4+4+1=10种方案.根据分类加法计数原理可得共有1+8+10=19种开课方案.

练习册系列答案
相关题目
 满足
满足 且
且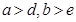 (如37201,45412),则称这个五位数符合“正弦规律”.那么,共有 个五位数符合“正弦规律”.
(如37201,45412),则称这个五位数符合“正弦规律”.那么,共有 个五位数符合“正弦规律”. 名优秀学生
名优秀学生 、
、 、
、 、
、 全部被保送到甲、乙、丙
全部被保送到甲、乙、丙 所学校,每所学校至少去一名,则不同的保送方案共有 种.
所学校,每所学校至少去一名,则不同的保送方案共有 种.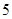 个程序,其中程序
个程序,其中程序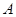 只能出现在第一步或最后一步,程序
只能出现在第一步或最后一步,程序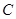 和
和 实施时必须相邻,则实验顺序的编排方法共有( )
实施时必须相邻,则实验顺序的编排方法共有( )