题目内容
(本小题满分10分)在直角坐标系xOy中,以原点O为圆心的圆与直线x-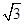 y-4=0相切,
y-4=0相切,
(Ⅰ)求圆O的方程;
(Ⅱ)若已知点P(3,2),过点P作圆O的切线,求切线的方程。
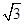 y-4=0相切,
y-4=0相切,(Ⅰ)求圆O的方程;
(Ⅱ)若已知点P(3,2),过点P作圆O的切线,求切线的方程。
(Ⅰ)x2+y2=4;(Ⅱ)12x-5y-26=0或y-2=0。
试题分析:(Ⅰ)设圆的方程为x2+y2=r2,
由题可知,半径即为圆心到切线的距离,故r=
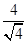 =2,
=2,∴圆的方程是x2+y2=4;
(Ⅱ) ∵|OP|=
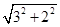 =
=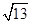 >2,∴点P在圆外.
>2,∴点P在圆外.显然,斜率不存在时,直线与圆相离。
故可设所求切线方程为y-2=k(x-3),即kx-y+2-3k=0.
又圆心为O(0,0),半径r=2,而圆心到切线的距离d=
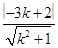 =2,即|3k-2|=2
=2,即|3k-2|=2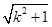 ,
,∴k=
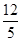 或k=0,
或k=0,故所求切线方程为12x-5y-26=0或y-2=0。
点评:充分利用直线与圆相切的性质来求直线方程,注意设直线方程点斜式的时候,一定要注意讨论直线的斜率是否存在。

练习册系列答案
相关题目
 ,直线
,直线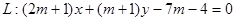
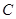 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时 的值及最短长度。
的值及最短长度。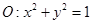 和点
和点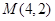 .
.
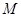 向⊙
向⊙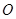 引切线
引切线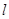 ,求直线
,求直线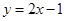 截得的弦长为4的⊙
截得的弦长为4的⊙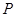 为(Ⅱ)中⊙
为(Ⅱ)中⊙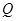 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点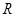 ,使得
,使得 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由. 
 三点的圆的方程,并指出圆心坐标与圆的半径.
三点的圆的方程,并指出圆心坐标与圆的半径.
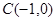 与条件 (1) 的圆相切的直线方程.
与条件 (1) 的圆相切的直线方程.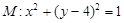 ,直线
,直线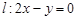 ,点
,点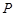 在直线
在直线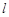 上,过点
上,过点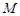 的切线
的切线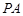 、
、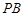 ,切点为
,切点为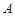 、
、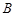 .
.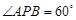 ,求
,求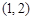 ,过
,过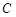 、
、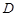 两点,当
两点,当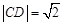 时,求直线
时,求直线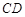 的方程;
的方程;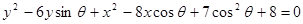 .
.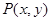 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求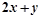 的取值范围.
的取值范围. 中,“直线
中,“直线 ,
, 与曲线
与曲线 相切”的充要条件是 .
相切”的充要条件是 . 的切线,则切线的方程为( )
的切线,则切线的方程为( )

 作两条切线,则该圆夹在两条切线间的劣弧长为 .
作两条切线,则该圆夹在两条切线间的劣弧长为 .