题目内容
已知二次函数f(x)=ax2+bx(a,b是常数,且a≠0),f(2)=0,且方程f(x)=x有两个相等的实数根.
(1)求f(x)的解析式;
(2)当x∈[0,3]时,求函数f(x)的值域.
(1)求f(x)的解析式;
(2)当x∈[0,3]时,求函数f(x)的值域.
分析:(1)由f(2)=0,且f(x)=x有两个相等的实数根,求出a、b的值,从而得f(x)的解析式;
(2)画出f(x)的图象,结合图象求出f(x)在x∈[0,3]时的最值,即得值域.
(2)画出f(x)的图象,结合图象求出f(x)在x∈[0,3]时的最值,即得值域.
解答:解:(1)∵f(2)=0,∴4a+2b=0①;
又方程f(x)=x有两个相等的实数根,
即ax2+(b-1)x=0有两个相等的实数根,
∴(b-1)2=0②;
由①②可得,a=-
,b=1,
∴f(x)=-
x2+x;
(2)由(1)知,f(x)=-
x2+x对称轴为=1,开口向下,
如图,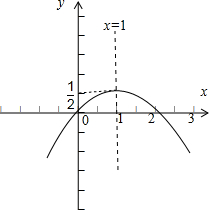 ;
;
由图可知,当∈[0,3]时,f(x)max=f(1)=
,f(x)min=f(3)=-
,
∴f(x)在x∈[0,3]时的值域是[-
,
].
又方程f(x)=x有两个相等的实数根,
即ax2+(b-1)x=0有两个相等的实数根,
∴(b-1)2=0②;
由①②可得,a=-
| 1 |
| 2 |
∴f(x)=-
| 1 |
| 2 |
(2)由(1)知,f(x)=-
| 1 |
| 2 |
如图,
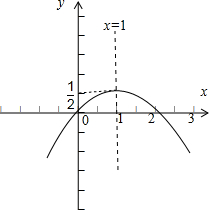 ;
;由图可知,当∈[0,3]时,f(x)max=f(1)=
| 1 |
| 2 |
| 3 |
| 2 |
∴f(x)在x∈[0,3]时的值域是[-
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题考查了求函数的解析式以及利用函数的图象与性质求最值,从而得值域的问题,是基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目