题目内容
设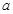 为实常数,
为实常数,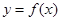 是定义在
是定义在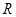 上的奇函数,当
上的奇函数,当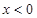 时,
时,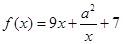 , 若
, 若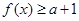 对一切
对一切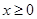 成立,则
成立,则 的取值范围为 .
的取值范围为 .
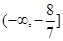 .
.
解析试题分析:∵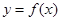 是定义在
是定义在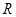 上的奇函数,∴当
上的奇函数,∴当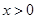 时,
时,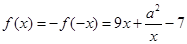 ,
,
而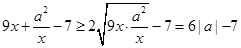 ,当些仅当
,当些仅当 时,“=”成立,∴当
时,“=”成立,∴当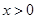 时,要使
时,要使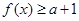 恒成立,只需
恒成立,只需 或
或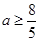 ,又∵
,又∵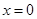 时,
时,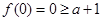 ,∴
,∴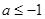 ,
,
综上,故实数 的取值范围是
的取值范围是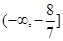 .
.
考点:1.奇函数的性质;2.恒成立问题的处理方法.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
函数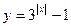 的定义域为
的定义域为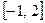 ,则其值域为
,则其值域为
A.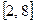 | B.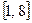 | C.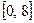 | D.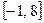 |
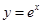 的图象与
的图象与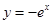 的图象关于
的图象关于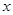 轴对称;
轴对称;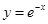 的图象关于
的图象关于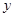 轴对称;
轴对称;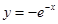 的图象关于坐标原点对称.
的图象关于坐标原点对称.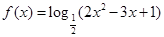 的增区间是____________.
的增区间是____________. 满足
满足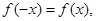 且当
且当 时总有
时总有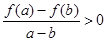 ,其中
,其中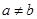 .
. 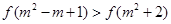 ,则实数
,则实数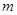 的取值范围是 .
的取值范围是 .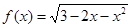 的定义域为 .
的定义域为 .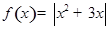 ,
,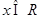 .若方程
.若方程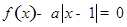 恰有4个互异的实数根,则实数
恰有4个互异的实数根,则实数 的取值范围为__________.
的取值范围为__________.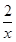 的零点,则[x0]等于________.
的零点,则[x0]等于________.