题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{-\frac{2}{x-1},x≤0}\\{(x-1)^{2},0<x≤2}\\{3-x,2<x<4}\end{array}\right.$(1)写出函数f(x)的定义域,值域;
(2)当方程f(x)=a有两解时,求a的值;
(3)当方程f(x)=a有最多解时,求a的取值范围.
分析 (1)先写出定义域,再分段求y的取值,从而求值域;
(2)根据(1)中的分析作出函数的图象,从而利用数形结合解得;
(3)利用数形结合解得.
解答 解:(1)函数f(x)的定义域为(-∞,4);
当x≤0时,0<-$\frac{2}{x-1}$≤2;
当0<x≤2时,0≤(x-1)2≤1;
当2<x<4时,-1<3-x<1;
故函数的值域为[-1,2].
(2)由(1)作出函数f(x)的图象如下,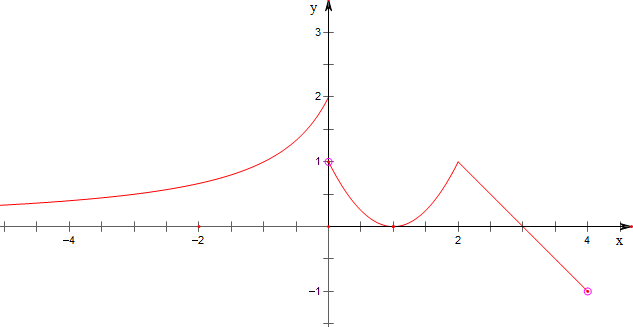
结合图象可知,当方程f(x)=a有两解时,a=1或a=0;
(3)结合图象可知,当方程f(x)=a有最多解时,
0<a<1.
点评 本题考查了分段函数的应用及数形结合的思想应用.

练习册系列答案
相关题目
10.已知集合A={x|x2-x-2≤0},B={y|y=2x},则A∩B=( )
| A. | (0,2] | B. | (0,1]. | C. | (-1,0] | D. | (0,4] |