题目内容
15.函数f(x)=$\sqrt{m{x}^{2}-2x+1}$的定义域为R,则实数m的取值范围是m≥1.分析 函数的定义域为R,则等价mx2-2x+1≥0恒成立,然后解不等式即可.
解答 解:∵函数f(x)的定义域为R,
∴mx2-2x+1≥0恒成立.
①若m=0,则不等式等价为-2x+1≥0,即x≤$\frac{1}{2}$,不满足条件.
②若m≠0,要使不等式恒成立,则$\left\{\begin{array}{l}{m>0}\\{△=4-4m≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m>0}\\{m≥1}\end{array}\right.$,解得m≥1,
综上m≥1,
故答案为:m≥1
点评 本题主要考查函数定义域的应用,利用函数定义域为R,得到mx2-2x+1≥0恒成立.是解决本题 的关键,利用二次函数和二次不等式之间的关系进行求解是突破点.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
10.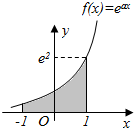 已知函数f(x)=eax(a为常数)的图象如下图所示,则图中阴影部分(曲线y=f(x)与x轴,直线x=-1,x=1所围成的封闭图形)的面积是( )
已知函数f(x)=eax(a为常数)的图象如下图所示,则图中阴影部分(曲线y=f(x)与x轴,直线x=-1,x=1所围成的封闭图形)的面积是( )
 已知函数f(x)=eax(a为常数)的图象如下图所示,则图中阴影部分(曲线y=f(x)与x轴,直线x=-1,x=1所围成的封闭图形)的面积是( )
已知函数f(x)=eax(a为常数)的图象如下图所示,则图中阴影部分(曲线y=f(x)与x轴,直线x=-1,x=1所围成的封闭图形)的面积是( )| A. | $\frac{{e}^{2}-{e}^{-2}}{2}$ | B. | $\frac{{e}^{2}+{e}^{-2}}{2}$ | C. | e2-e-2 | D. | e2+e-2 |