题目内容
设P是焦点为F1、F2椭圆 >b>0)上的任意一点,若∠F1PF2的最大值为60°,方程ax2+bx-c=0的两个实根分别为x1和x2,则过点P(x1,x2)引圆x2+y2=2的切线共有 条.
>b>0)上的任意一点,若∠F1PF2的最大值为60°,方程ax2+bx-c=0的两个实根分别为x1和x2,则过点P(x1,x2)引圆x2+y2=2的切线共有 条.
【答案】分析:当P在椭圆的短轴顶点时,∠F1PF2的最大值,用c表示出a和b,化简一元二次方程,求出根,得到点P的坐标,看点P到圆心的距离与半径的关系,确定切线数量.
解答:解:当P在椭圆的短轴顶点时,∠F1PF2的最大值为60°,∴a=2c,b=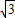 c,
c,
方程ax2+bx-c=0 即 2cx2+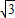 cx-c=0,即 2x2+
cx-c=0,即 2x2+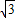 x-1=0,此方程的2个根是
x-1=0,此方程的2个根是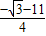 、
、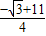 ,
,
点P( ,
,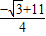 )到圆心的距离为
)到圆心的距离为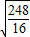 =
=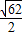 >半径
>半径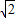 ,
,
点P在圆外,则切线由2条;
故答案为2.
点评:本题考查椭圆的性质及圆的切线方程.
解答:解:当P在椭圆的短轴顶点时,∠F1PF2的最大值为60°,∴a=2c,b=
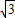 c,
c,方程ax2+bx-c=0 即 2cx2+
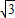 cx-c=0,即 2x2+
cx-c=0,即 2x2+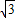 x-1=0,此方程的2个根是
x-1=0,此方程的2个根是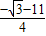 、
、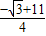 ,
,点P(
 ,
,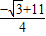 )到圆心的距离为
)到圆心的距离为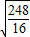 =
=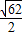 >半径
>半径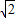 ,
,点P在圆外,则切线由2条;
故答案为2.
点评:本题考查椭圆的性质及圆的切线方程.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 给出以下判断:
给出以下判断:
 的离心率为
的离心率为 ,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.
,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.