题目内容
15.已知球O的表面积为12π,则球O的体积为( )| A. | 2$\sqrt{3}$π | B. | 4$\sqrt{3}$π | C. | 12$\sqrt{3}$π | D. | 32$\sqrt{3}$π |
分析 先利用球的表面积计算公式,求得球的半径,再利用球的体积计算公式计算球的体积即可
解答 解:设球的半径为r,依题意:
球的表面积s=4πr2=12π,解得r=$\sqrt{3}$,
∴该球的体积V=$\frac{4}{3}$πr3=$\frac{4}{3}$π×$(\sqrt{3})^{3}$=4$\sqrt{3}$π,
故选:B.
点评 本题考查了球的表面积、体积计算公式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
5.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
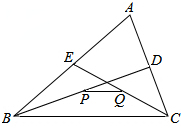

| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
6.高为1的四棱锥S-ABCD的底面是边长为2的正方形,点S、A、B、C、D均在半径为$\frac{\sqrt{17}}{2}$的同一球面上,在底面ABCD的中心与顶点S之间的距离为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{2}$ |
10.已知α∩β=l,a?α,b?β,且a,b是异面直线,那么直线l( )
| A. | 至多与a,b中的一条相交 | B. | 至少与a,b中的一条平行 | ||
| C. | 与a,b都相交 | D. | 至少与a,b中的一条相交 |
5.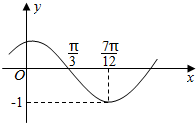 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,0<ϕ<π)的图象如图所示,为了得到g(x)=Asinωx的图象,可将f(x)的图象( )
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,0<ϕ<π)的图象如图所示,为了得到g(x)=Asinωx的图象,可将f(x)的图象( )
 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,0<ϕ<π)的图象如图所示,为了得到g(x)=Asinωx的图象,可将f(x)的图象( )
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,0<ϕ<π)的图象如图所示,为了得到g(x)=Asinωx的图象,可将f(x)的图象( )| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |